题目内容
15. 二次函数y=ax2+bx+c(a≠0)和正比例函数y=$\frac{2}{3}$x的图象如图所示,则方程ax2+(b-$\frac{2}{3}$)x+c=0(a≠0)的根的情况( )
二次函数y=ax2+bx+c(a≠0)和正比例函数y=$\frac{2}{3}$x的图象如图所示,则方程ax2+(b-$\frac{2}{3}$)x+c=0(a≠0)的根的情况( )| A. | 两根都大于0 | B. | 两根都等于0 | ||
| C. | 两根都小于0 | D. | 一根大于0,一根小于0 |
分析 设ax2+bx+c=0(a≠0)的两根为x1,x2,由二次函数的图象可知x1+x2>0,a>0,设方程ax2+(b-$\frac{2}{3}$)x+c=0(a≠0)的两根为m,n再根据根与系数的关系即可得出结论.
解答 解:设ax2+bx+c=0(a≠0)的两根为x1,x2,
∵由二次函数的图象可知x1x2<0,
∴$\frac{c}{a}$<0.
设方程ax2+(b-$\frac{2}{3}$)x+c=0(a≠0)的两根为m,n,则mn=$\frac{c}{a}$<0,
∴方程ax2+(b-$\frac{2}{3}$)x+c=0(a≠0)的两根为一根大于0,一根小于0,
故选D.
点评 本题考查的是抛物线与x轴的交点,熟知抛物线与x轴的交点与一元二次方程根的关系是解答此题的关键.

练习册系列答案
相关题目
6.下列方程中是一元一次方程的是( )
| A. | xy=2 | B. | 2x2-x-1=0 | C. | x-2y=4 | D. | 3(2x-7)=4(x-5) |
6.若关于x的一元二次方程(m+3)x2+(m2-2m-5)x+m-7=0有一解是1,则m的值为( )
| A. | ±3 | B. | -3 | C. | 3 | D. | $-\frac{2}{3}$ |
3.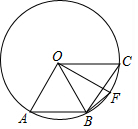 如图,点A、B、C是圆O上的三点,且四边形ABCO是平行四边形,OF⊥OA交圆O于点F,则∠CBF等于( )
如图,点A、B、C是圆O上的三点,且四边形ABCO是平行四边形,OF⊥OA交圆O于点F,则∠CBF等于( )
 如图,点A、B、C是圆O上的三点,且四边形ABCO是平行四边形,OF⊥OA交圆O于点F,则∠CBF等于( )
如图,点A、B、C是圆O上的三点,且四边形ABCO是平行四边形,OF⊥OA交圆O于点F,则∠CBF等于( )| A. | 12.5° | B. | 15° | C. | 20° | D. | 22.5° |
20.用代数式表示“m的3倍与n的平方差”,正确的是( )
| A. | (3m-n)2 | B. | 3(m-n)2 | C. | (3m)2-n2 | D. | (m-3n)2 |
7.下列各组整式中,不是同类项的是( )
| A. | 3x2y与-$\frac{1}{3}$x2y | B. | -$\frac{1}{3}$与0 | C. | xyz3与-xyz3 | D. | 2x3y与2xy3 |
3.对抛物线y=-x2+2x-3而言,下列结论正确的是( )
| A. | 与x轴有两个公共点; | |
| B. | 与y轴的交点坐标是(0,3); | |
| C. | 当x<1时,y随x的增大而增大;当x>1时,y随x的增大而减小; | |
| D. | 开口向上. |