题目内容
14．一元二次方程5x2-11x+4=0的根的情况是（ ）| A． | 有两个相等的实数根 | B． | 有两个不相等的实数根 | ||
| C． | 只有一个实数根 | D． | 没有实数根 |
分析 根据根的判别式找出△=41＞0，由此即可得出结论．
解答 解：∵在方程5x2-11x+4=0中，△=（-11）2-4×5×4=41＞0，
∴方程5x2-11x+4=0有两个不相等的实数根．
故选B．
点评 本题考查了根的判别式，根据根的判别式找出△=41＞0是解题的关键．
练习册系列答案
相关题目
7．下列等式由左到右的变形是因式分解的是（ ）
| A． | a2-b2+1=（a+b）（a-b）+1 | B． | xy（x2+y2）（x+y）（x-y）=x5y-xy5 | ||
| C． | （m+3）2=m2+9 | D． | x2-9=（x+3）（x-3） |
6．下列方程中是一元一次方程的是（ ）
| A． | xy=2 | B． | 2x2-x-1=0 | C． | x-2y=4 | D． | 3（2x-7）=4（x-5） |
2．
二次函数y=ax2+bx+c（a≠0）的图象如图所示，则点M（a，b+c）在（ ）
二次函数y=ax2+bx+c（a≠0）的图象如图所示，则点M（a，b+c）在（ ）| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
9．
如图，AB是⊙O的直径，点C在⊙O上，连接AC、BC，点D是BA延长线上一点，且AC=AD，若∠B=30°，AB=2，则CD的长是（ ）
如图，AB是⊙O的直径，点C在⊙O上，连接AC、BC，点D是BA延长线上一点，且AC=AD，若∠B=30°，AB=2，则CD的长是（ ）| A． | $\sqrt{5}$ | B． | 2 | C． | 1 | D． | $\sqrt{3}$ |
6．若关于x的一元二次方程（m+3）x2+（m2-2m-5）x+m-7=0有一解是1，则m的值为（ ）
| A． | ±3 | B． | -3 | C． | 3 | D． | $-\frac{2}{3}$ |
3．
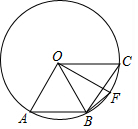如图，点A、B、C是圆O上的三点，且四边形ABCO是平行四边形，OF⊥OA交圆O于点F，则∠CBF等于（ ）
如图，点A、B、C是圆O上的三点，且四边形ABCO是平行四边形，OF⊥OA交圆O于点F，则∠CBF等于（ ）| A． | 12.5° | B． | 15° | C． | 20° | D． | 22.5° |
3．对抛物线y=-x2+2x-3而言，下列结论正确的是（ ）
| A． | 与x轴有两个公共点； | |
| B． | 与y轴的交点坐标是（0，3）； | |
| C． | 当x＜1时，y随x的增大而增大；当x＞1时，y随x的增大而减小； | |
| D． | 开口向上． |