题目内容
11. 如图,在△ABC中,DE∥BC,$\frac{AD}{BD}$=$\frac{1}{2}$,BC=12,则DE的长是( )
如图,在△ABC中,DE∥BC,$\frac{AD}{BD}$=$\frac{1}{2}$,BC=12,则DE的长是( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
分析 因为DE∥BC,所以可以判断△ADE∽△ABC,根据AD:BD=1:2即可得出结论.
解答 解:∵AD:BD=1:2,
∴AD:AB=1:3,
∵DE∥BC,
∴△ADE∽△ABC,
∴$\frac{DE}{BC}$=$\frac{AD}{AB}$=$\frac{1}{3}$,
∵BC=12,
∴DE=4,
故选B.
点评 本题考查了相似三角形的判定和性质,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
3.对抛物线y=-x2+2x-3而言,下列结论正确的是( )
| A. | 与x轴有两个公共点; | |
| B. | 与y轴的交点坐标是(0,3); | |
| C. | 当x<1时,y随x的增大而增大;当x>1时,y随x的增大而减小; | |
| D. | 开口向上. |
6.已知2是关于x的方程x2+ax-3a=0的根,则a的值为( )
| A. | -4 | B. | 4 | C. | 2 | D. | $\frac{4}{5}$ |
18.下列计算正确的是( )
| A. | 5m-2m=3 | B. | 6x3+4x7=10x10 | C. | 3a+2a=5a2 | D. | 8a2b-8ba2=0 |
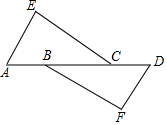 如图,AE∥DF,AB=DC,不再添加辅助线和字母,要使△EAC≌△FDB,需添加的一个条件是∠E=∠F或AE=DF(只写一个条件即可)
如图,AE∥DF,AB=DC,不再添加辅助线和字母,要使△EAC≌△FDB,需添加的一个条件是∠E=∠F或AE=DF(只写一个条件即可)