题目内容
18.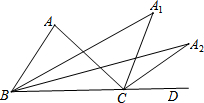 如图,在△ABC中,∠A=96°,延长BC至D,∠ABC与∠ACD的平分线相交于点A1,∠A1BC与∠A1CD的平分线相交于点A2,依此类推,∠A4BC与∠A4CD的平分线相交于点A5,则∠A5的度数为( )
如图,在△ABC中,∠A=96°,延长BC至D,∠ABC与∠ACD的平分线相交于点A1,∠A1BC与∠A1CD的平分线相交于点A2,依此类推,∠A4BC与∠A4CD的平分线相交于点A5,则∠A5的度数为( )| A. | 3° | B. | 6° | C. | 19.2° | D. | 24° |
分析 利用角平分线的定义和三角形内角与外角的性质计算.
解答 解:∵∠BA1C+∠A1BC=∠A1CD,2∠A1CD=∠ACD=∠BAC+∠ABC,
∴2(∠BA1C+∠A1BC)=∠BAC+∠ABC,2∠BA1C+2∠A1BC=∠BAC+∠ABC.
∵2∠A1BC=∠ABC,
∴2∠BA1C=∠BAC.
同理,可得2∠BA2C=∠BA1C,2∠BA3C=∠BA2C,2∠BA4C=∠BA3C,2∠BA5C=∠BA4C,
∴∠BA5C=$\frac{1}{2}$∠BA4C=$\frac{1}{4}$∠BA3C=$\frac{1}{8}$∠BA2C=$\frac{1}{16}$∠BA1C=$\frac{1}{32}$∠BAC=96°÷32=3°.
故选A.
点评 本题考查了三角形的内角和定理,即三角形的内角和为180°.也考查了三角形的外角性质以及角平分线性质,难度适中.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
9. 如图,AB是⊙O的直径,点C在⊙O上,连接AC、BC,点D是BA延长线上一点,且AC=AD,若∠B=30°,AB=2,则CD的长是( )
如图,AB是⊙O的直径,点C在⊙O上,连接AC、BC,点D是BA延长线上一点,且AC=AD,若∠B=30°,AB=2,则CD的长是( )
 如图,AB是⊙O的直径,点C在⊙O上,连接AC、BC,点D是BA延长线上一点,且AC=AD,若∠B=30°,AB=2,则CD的长是( )
如图,AB是⊙O的直径,点C在⊙O上,连接AC、BC,点D是BA延长线上一点,且AC=AD,若∠B=30°,AB=2,则CD的长是( )| A. | $\sqrt{5}$ | B. | 2 | C. | 1 | D. | $\sqrt{3}$ |
7.下列各组整式中,不是同类项的是( )
| A. | 3x2y与-$\frac{1}{3}$x2y | B. | -$\frac{1}{3}$与0 | C. | xyz3与-xyz3 | D. | 2x3y与2xy3 |
14.下列命题:
①一腰和底边对应相等的两个等腰三角形全等;
②腰长相等,且都有一个40°角的两个等腰三角形全等;
③腰长相等,且都有一个100°角的两个等腰三角形全等;
④腰和定焦对应相等的两个等腰三角形全等;
⑤两个等边三角形全等;
其中正确的命题的个数有( )
①一腰和底边对应相等的两个等腰三角形全等;
②腰长相等,且都有一个40°角的两个等腰三角形全等;
③腰长相等,且都有一个100°角的两个等腰三角形全等;
④腰和定焦对应相等的两个等腰三角形全等;
⑤两个等边三角形全等;
其中正确的命题的个数有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
3.对抛物线y=-x2+2x-3而言,下列结论正确的是( )
| A. | 与x轴有两个公共点; | |
| B. | 与y轴的交点坐标是(0,3); | |
| C. | 当x<1时,y随x的增大而增大;当x>1时,y随x的增大而减小; | |
| D. | 开口向上. |
9.已知△ABC中,a、b、c分别是∠A、∠B、∠C的对边,下列条件不能判断△ABC是直角三角形的是( )
| A. | a:b:c=4:5:6 | B. | b 2=a2-c2 | C. | ∠A=∠C-∠B | D. | a=3,b=4,c=5 |
6.已知2是关于x的方程x2+ax-3a=0的根,则a的值为( )
| A. | -4 | B. | 4 | C. | 2 | D. | $\frac{4}{5}$ |