题目内容
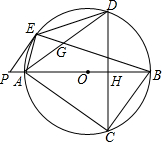 如图,点O是四边形AEBC外接圆的圆心,点O在AB上,点P在BA的延长线上,且∠PEA=∠ADE,CD⊥AB于点H,交⊙O于点D.
如图,点O是四边形AEBC外接圆的圆心,点O在AB上,点P在BA的延长线上,且∠PEA=∠ADE,CD⊥AB于点H,交⊙O于点D.(1)求证:PE是⊙O的切线;
(2)若D为劣弧
 |
| BE |
考点:切线的判定
专题:
分析:(1)利用等腰三角形的性质得出,∠OAE=∠OEA,进而利用圆周角定理得出答案;
(2)首先得出△END≌△CNB(AAS),进而得出BE=DC,进而求出即可.
(2)首先得出△END≌△CNB(AAS),进而得出BE=DC,进而求出即可.
解答:(1)证明:连接OE,
∵OA=OE,∴∠OAE=∠OEA,
∵∠PAE=∠ADE=∠ABE,
∴∠PAE+∠OEA=∠ABE+∠OAE,
∵AB为⊙O的直径,
∴∠ABE=90°,
∴∠PEO=90°,
∴PE是⊙O的切线;
(2)解:连接BD,
∵AH=16,BH=9,AB为⊙O的直径,
∴DH=12,
∵D是劣弧BE的中点,
∴∠CDB=∠DBE=∠EAD=∠BAD,
∴ND=NB,
在△END和△CNB中,
,
∴△END≌△CNB(AAS),
∴EN=NC,
∴BE=DC,
∴DH=HC=12,
∴BE=DC=24.
∵OA=OE,∴∠OAE=∠OEA,
∵∠PAE=∠ADE=∠ABE,
∴∠PAE+∠OEA=∠ABE+∠OAE,
∵AB为⊙O的直径,
∴∠ABE=90°,

∴∠PEO=90°,
∴PE是⊙O的切线;
(2)解:连接BD,
∵AH=16,BH=9,AB为⊙O的直径,
∴DH=12,
∵D是劣弧BE的中点,
∴∠CDB=∠DBE=∠EAD=∠BAD,
∴ND=NB,
在△END和△CNB中,
|
∴△END≌△CNB(AAS),
∴EN=NC,
∴BE=DC,
∴DH=HC=12,
∴BE=DC=24.
点评:此题主要考查了切线的判定以及全等三角形的判定与性质等知识,得出△END≌△CNB是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 二次函数y=ax2+bx+c(a≠0)的图象如图,则下列结论中正确的是( )
二次函数y=ax2+bx+c(a≠0)的图象如图,则下列结论中正确的是( )| A、c>-1 |
| B、9a+c>3b |
| C、2a+b≠0 |
| D、b>0 |
已知点O是△ABC的外心,且∠ABC+∠ACB=100°,则∠BOC=( )
| A、100° |
| B、100°或80° |
| C、130° |
| D、160° |
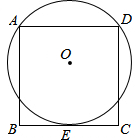 如图,正方形ABCD的边BC与⊙O相切于点E,点A、D在⊙O上.若AB=10,则⊙O的半径是
如图,正方形ABCD的边BC与⊙O相切于点E,点A、D在⊙O上.若AB=10,则⊙O的半径是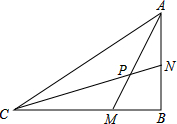 如图,△ABC是直角三角形,CM=AB,BM=AN,求∠CPM.
如图,△ABC是直角三角形,CM=AB,BM=AN,求∠CPM.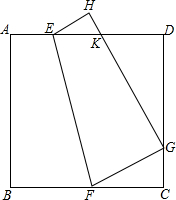 已知:正方形ABCD沿EF折叠,A与H,B与G分别重合,求证:AK+CG=GK.
已知:正方形ABCD沿EF折叠,A与H,B与G分别重合,求证:AK+CG=GK.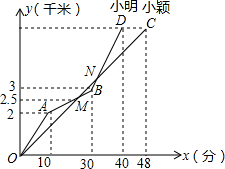 小明、小颖两名同学在学校冬季越野赛中的路程y(千米)与时间x(分)的函数关系如图所示.
小明、小颖两名同学在学校冬季越野赛中的路程y(千米)与时间x(分)的函数关系如图所示. 如图,以△ABC的三边为边分别作等边三角形△ADB、△BCF、△ACE.求证:DF=AE.
如图,以△ABC的三边为边分别作等边三角形△ADB、△BCF、△ACE.求证:DF=AE.