题目内容
15．已知一个正多边形的一个中心角为18°．求它的内角的度数．分析 正多边形的中心角=$\frac{360°}{n}$，先求出n，再根据内角和公式求出每个内角，也可以利用正多边形的外角等于中心角进行计算．
解答 解：设这个正多边形是正n边形，
由题意：$\frac{360°}{n}$=18°，
∴n=20，
∴正多边形每个内角的度数=$\frac{（20-2）×180°}{20}$=162°．
也可以利用正多边形的外角=18°，所以每个内角=180°-18°=162°．
点评 本题考查正多边形和圆的位置关系，知道正多边形的外角等于中心角，中心角=$\frac{360°}{n}$，属于中考常考题型．
练习册系列答案
名校课堂系列答案
相关题目
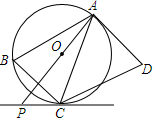如图，四边形ABCD是平行四边形，⊙O是△ABC的外接圆，AD与⊙O相切于点A，AO的延长线与过点C的直线相交于点P，且∠PCB=∠ACD．
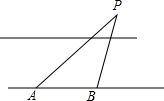在沿东西走向的河岸南岸，某人自西向东行走，在A处测得河北岸建筑物P在北偏东60°的方向上，某人由A向东走400米到达B处时，在B处测得河北岸物P在北偏东45°的方向上，如果建筑物P距河北岸100米，求河宽．（人与河的距离忽略不计，$\sqrt{3}$≈1.7）
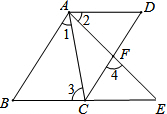如图，AB∥CD，AD∥BE，∠1=∠2，证明：∠3=∠4．
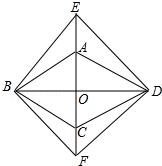如图，菱形ABCD的对角线AC，BD相交于点O，分别延长OA，OC到点E，F，使AE=CF，依次连接B，F，D，E各点．