题目内容
3．
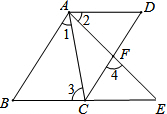如图，AB∥CD，AD∥BE，∠1=∠2，证明：∠3=∠4．
分析 根据平行线的性质得到∠3=∠CAD，根据等式的性质得到∠BAE=∠CAD．根据平行线的性质得到∠4=∠BAE，等量代换即可得到结论．
解答 证明：∵AD∥BE，
∴∠3=∠CAD（ 两直线平行，内错角相等），
∵∠1=∠2．
∴∠1+∠CAE=∠2+∠CAE．
即∠BAE=∠CAD．
∵AB∥CD，
∴∠4=∠BAE（ 两直线平行，同位角相等），
∴∠3=∠4．
点评 本题主要考查平行线的性质，掌握平行线的性质和判定是解题的关键，即①两直线平行?同位角相等，②两直线平行?内错角相等，③两直线平行?同旁内角互补，④a∥b，b∥c⇒a∥c．
练习册系列答案
相关题目
18．在（$\frac{2}{3}$）2，（$\frac{3}{4}$）-2，（$\frac{6}{5}$）2，（$\frac{6}{7}$）0这四个数中，最小的是（ ）
| A． | （$\frac{2}{3}$）2 | B． | （$\frac{3}{4}$）-2 | C． | （$\frac{6}{5}$）2 | D． | （$\frac{6}{7}$）0 |
8．若（x-1）0-2（x-2）-2无意义，则x的取值范围是（ ）
| A． | x≠1且x≠2 | B． | x≠1或x≠2 | C． | x=1且x=2 | D． | x=1或x=2 |
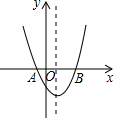如图，抛物线y=2x2+mx-3的顶点横坐标是1，它与x轴交于A、B两点，点A的坐标是（-1，0），那么关于x的方程2x2+mx-3=0的两根和是（ ）
12．（-3）0等于（ ）
| A． | 1 | B． | -1 | C． | -3 | D． | 0 |