题目内容
16.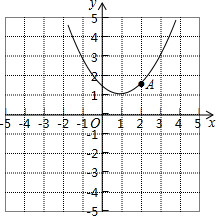 如图,抛物线y=$\frac{1}{2}$x2-x+c和反比例函数y=$\frac{k}{x}$的图象都经过A(2,1.5).
如图,抛物线y=$\frac{1}{2}$x2-x+c和反比例函数y=$\frac{k}{x}$的图象都经过A(2,1.5).(1)求抛物线顶点坐标;
(2)在同一坐标系中画出函数y=$\frac{k}{x}$的图象;
(3)根据函数图象,直接写出:
①方程$\frac{1}{2}$x2-x+$\frac{3}{2}$=$\frac{3}{x}$实数根的个数;
②不等式$\frac{1}{2}$x2-x+$\frac{3}{2}$$>\frac{3}{x}$的解集.
分析 (1)利用待定系数法求出二次函数的解析式即可解决问题;
(2)利用描点法画出函数图象即可;
(3)①②利用图象法即可解决问题;
解答 解:(1)∵抛物线y=$\frac{1}{2}$x2-x+c和反比例函数y=$\frac{k}{x}$的图象都经过A(2,1.5).
∴1.5=2-2+c,k=3,
∴c=1.5,k=3,
∴y=$\frac{1}{2}$x2-x+$\frac{3}{2}$=$\frac{1}{2}$(x-1)2+1,
∴抛物线的顶点坐标为(1,1).
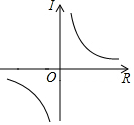
(2)y=$\frac{3}{x}$,图象如图所示,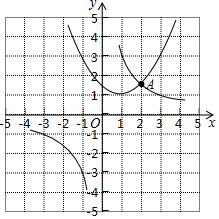
(3)①由图象可知,方程$\frac{1}{2}$x2-x+$\frac{3}{2}$=$\frac{3}{x}$实数根的个数为1.
②由图象可知,不等式$\frac{1}{2}$x2-x+$\frac{3}{2}$$>\frac{3}{x}$的解集为x>2.
点评 本题考查二次函数与不等式组、反比例函数的图象、二次函数的性质等知识,解题的关键是灵活运用所学知识解决问题,学会利用图象解决实际问题.

练习册系列答案
相关题目
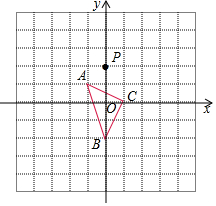 如图,在平面直角坐标系中,△ABC的顶点坐标分别为A(-1,1),B(0,-2),C(1,0),点P(0,2)绕点A旋转180°得到点P1,点P1绕点B旋转180°得到点P2,点P2绕点C旋转180°得到点P3,点P3绕点A旋转180°得到点P4,…,按此作法进行下去,则点P2017的坐标为(-2,0).
如图,在平面直角坐标系中,△ABC的顶点坐标分别为A(-1,1),B(0,-2),C(1,0),点P(0,2)绕点A旋转180°得到点P1,点P1绕点B旋转180°得到点P2,点P2绕点C旋转180°得到点P3,点P3绕点A旋转180°得到点P4,…,按此作法进行下去,则点P2017的坐标为(-2,0).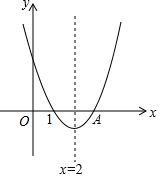 二次函数y=ax2+bx+c(a≠0)的图象的对称轴是直线x=2,且经过点A(3,0),根据图象解答下列问题:
二次函数y=ax2+bx+c(a≠0)的图象的对称轴是直线x=2,且经过点A(3,0),根据图象解答下列问题: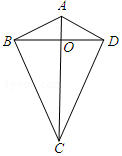 两组邻边分别相等的四边形我们称它为筝形.如图,在四边形ABCD中,AB=AD,BC=DC,AC与BD相交于点O,下列判断正确的有( )
两组邻边分别相等的四边形我们称它为筝形.如图,在四边形ABCD中,AB=AD,BC=DC,AC与BD相交于点O,下列判断正确的有( ) 定义:有三个内角相等的四边形叫三等角四边形.
定义:有三个内角相等的四边形叫三等角四边形. 一次函数y=ax+b和反比例函数y=$\frac{b}{x}$在同一坐标系内的大致图象如图所示,则a<0,b>0.
一次函数y=ax+b和反比例函数y=$\frac{b}{x}$在同一坐标系内的大致图象如图所示,则a<0,b>0.