题目内容
4.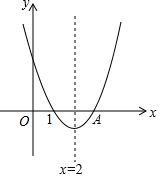 二次函数y=ax2+bx+c(a≠0)的图象的对称轴是直线x=2,且经过点A(3,0),根据图象解答下列问题:
二次函数y=ax2+bx+c(a≠0)的图象的对称轴是直线x=2,且经过点A(3,0),根据图象解答下列问题:(1)方程ax2+bx+c=0的两个根是1或3;
(2)不等式ax2+bx+c>0的解集是x<1或x>3;
(3)y随x的增大而减小的自变量x的取值范围是x<2;
(4)若方程ax2+bx+c=k有两个不相等的实数根,且与y轴交于点C(0,3),求实数k的取值范围.
分析 (1)二次函数y=ax2+bx+c(a≠0)与x轴交点的横坐标,即为方程ax2+bx+c(a≠0)=0的根;
(2)观察图象可知,不等式ax2+bx+c>0的解,就是抛物线的图象在x轴的上方部分;
(3)观察图象即可解决问题;
(4)方程ax2+bx+c=k有两个不相等的实数根,即直线y=k与抛物线y=x2-4x+3有两个交点,观察图象即可解决问题.
解答 解:(1)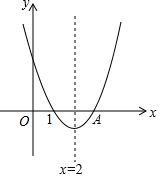 ∵二次函数y=ax2+bx+c(a≠0)的图象的对称轴是直线x=2,且经过点A(3,0),
∵二次函数y=ax2+bx+c(a≠0)的图象的对称轴是直线x=2,且经过点A(3,0),
∴二次函数与x轴的另一个交点坐标为(1,0),
∴方程ax2+bx+c=0的两个根是1或3,
故答案为1或3.
(2)观察图象可知,不等式ax2+bx+c>0的解集是x<1或x>3.
故答案为x<1或x>3.
(3)y随x的增大而减小的自变量x的取值范围是x<2.
故答案为x<2.
(4)由题意易知抛物线的解析式为y=x2-4x+3,
∴顶点坐标(2,-1),
观察图象可知,方程ax2+bx+c=k有两个不相等的实数根,即直线y=k与抛物线y=x2-4x+3有两个交点,
∴k>-1.
点评 本题考查二次函数与不等式、二次函数的性质、抛物线与x轴的交点等知识,解题的关键是灵活运用所学知识解决问题,学会利用图象解决实际问题,属于中考常考题型.

练习册系列答案
相关题目
13.下列图形中既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
9. 将一副三角板如图所示放置,且满足BC∥DE,则∠AFC=( )
将一副三角板如图所示放置,且满足BC∥DE,则∠AFC=( )
 将一副三角板如图所示放置,且满足BC∥DE,则∠AFC=( )
将一副三角板如图所示放置,且满足BC∥DE,则∠AFC=( )| A. | 80° | B. | 75° | C. | 70° | D. | 65° |
13.已知关于x,y的二元一次方程组$\left\{\begin{array}{l}{3x+2y=a+2}\\{2x+3y=a}\end{array}\right.$的解满足x与y之和为2,求a的值.
14.关于x的一元二次方程(a+1)x2-x+a2-2a-2=0,有一个根是1,则a=( )
| A. | -1 | B. | 2 | C. | 2或-1 | D. | -2或1 |
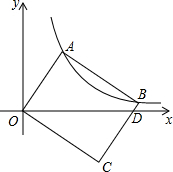 如图,在平面直角坐标系xOy,矩形OABC的顶点A、B在双曲线y=$\frac{k}{x}$(x>0)上.若点A的坐标为(1,2),则点B坐标为(4,$\frac{1}{2}$).
如图,在平面直角坐标系xOy,矩形OABC的顶点A、B在双曲线y=$\frac{k}{x}$(x>0)上.若点A的坐标为(1,2),则点B坐标为(4,$\frac{1}{2}$).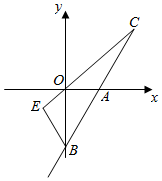 如图,直线y=2x-4与x轴交于点A,与y轴交于点B,与直线y=$\frac{1}{2}$x交于点C,E为射线CO上一点,且y轴平分∠EBC,求点E的坐标.
如图,直线y=2x-4与x轴交于点A,与y轴交于点B,与直线y=$\frac{1}{2}$x交于点C,E为射线CO上一点,且y轴平分∠EBC,求点E的坐标.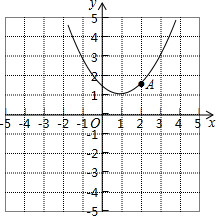 如图,抛物线y=$\frac{1}{2}$x2-x+c和反比例函数y=$\frac{k}{x}$的图象都经过A(2,1.5).
如图,抛物线y=$\frac{1}{2}$x2-x+c和反比例函数y=$\frac{k}{x}$的图象都经过A(2,1.5).