题目内容
1.已知二次函数y=a(x-m)2-a(x-m)(其中a,m为常数,且a>0).请把y=a(x-m)2-a(x-m)直接化为y=a(x-x1)(x-x2)的形式,并说明该函数的图象与x轴总有两个公共点.分析 提取公因数a(x-m),即可将y=a(x-m)2-a(x-m)变形为y=a(x-m)(x-m-1),令y=0,即可求出方程a(x-m)2-a(x-m)=0的两个根为x1=m、x1=m+1,由m≠m+1,即可得出方程a(x-m)2-a(x-m)=0有两个不相等的实数根,进而即可得出二次函数y=a(x-m)2-a(x-m)的图象与x轴总有两个公共点.
解答 解:y=a(x-m)2-a(x-m)=a(x-m)(x-m-1).
令y=0,则有a(x-m)2-a(x-m)=a(x-m)(x-m-1)=0,
解得:x1=m,x2=m+1.
∵m≠m+1,
∴方程a(x-m)2-a(x-m)=0有两个不相等的实数根,
∴二次函数y=a(x-m)2-a(x-m)的图象与x轴总有两个公共点.
点评 本题考查了抛物线与x轴的交点以及二次函数的三种形式,将二次函数的解析式由一般式变形为交点式是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
9. 将一副三角板如图所示放置,且满足BC∥DE,则∠AFC=( )
将一副三角板如图所示放置,且满足BC∥DE,则∠AFC=( )
 将一副三角板如图所示放置,且满足BC∥DE,则∠AFC=( )
将一副三角板如图所示放置,且满足BC∥DE,则∠AFC=( )| A. | 80° | B. | 75° | C. | 70° | D. | 65° |
13.已知关于x,y的二元一次方程组$\left\{\begin{array}{l}{3x+2y=a+2}\\{2x+3y=a}\end{array}\right.$的解满足x与y之和为2,求a的值.
10.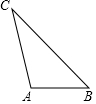 如图,△ABC是一块三条边长均不相等的薄板,要在△ABC薄板中裁剪出一个面积最大的圆形薄板,则圆形薄板的圆心应是△ABC的( )
如图,△ABC是一块三条边长均不相等的薄板,要在△ABC薄板中裁剪出一个面积最大的圆形薄板,则圆形薄板的圆心应是△ABC的( )
 如图,△ABC是一块三条边长均不相等的薄板,要在△ABC薄板中裁剪出一个面积最大的圆形薄板,则圆形薄板的圆心应是△ABC的( )
如图,△ABC是一块三条边长均不相等的薄板,要在△ABC薄板中裁剪出一个面积最大的圆形薄板,则圆形薄板的圆心应是△ABC的( )| A. | 三条高的交点 | B. | 三条中线的交点 | ||
| C. | 三边垂直平分线的交点 | D. | 三个内角角平分线的交点 |
11.下列各式化简后的结果为3$\sqrt{2}$的是( )
| A. | $\sqrt{6}$ | B. | $\sqrt{12}$ | C. | $\sqrt{18}$ | D. | $\sqrt{36}$ |
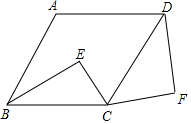 如图,在菱形ABCD中,∠A=110°,点E是菱形ABCD内一点,连结CE绕点C顺时针旋转110°,得到线段CF,连结BE,DF,若∠E=86°,求∠F的度数.
如图,在菱形ABCD中,∠A=110°,点E是菱形ABCD内一点,连结CE绕点C顺时针旋转110°,得到线段CF,连结BE,DF,若∠E=86°,求∠F的度数.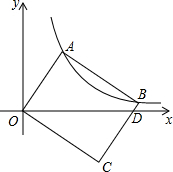 如图,在平面直角坐标系xOy,矩形OABC的顶点A、B在双曲线y=$\frac{k}{x}$(x>0)上.若点A的坐标为(1,2),则点B坐标为(4,$\frac{1}{2}$).
如图,在平面直角坐标系xOy,矩形OABC的顶点A、B在双曲线y=$\frac{k}{x}$(x>0)上.若点A的坐标为(1,2),则点B坐标为(4,$\frac{1}{2}$).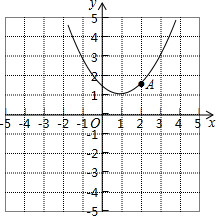 如图,抛物线y=$\frac{1}{2}$x2-x+c和反比例函数y=$\frac{k}{x}$的图象都经过A(2,1.5).
如图,抛物线y=$\frac{1}{2}$x2-x+c和反比例函数y=$\frac{k}{x}$的图象都经过A(2,1.5).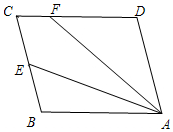 如图,平行四边形ABCD中,E是BC边的中点,连接AE、F为CD边上一点,且满足∠DFA=2∠BAE.
如图,平行四边形ABCD中,E是BC边的中点,连接AE、F为CD边上一点,且满足∠DFA=2∠BAE.