题目内容
如图,在方格纸中,△ABC的三个顶点及D、E、F、G、H、五个点分别位于小正方形的顶点上.
(1)画出△ABC绕点B顺时针方向旋转90°后的图形.
(2)先从E、F、G、H四个点中任意取两个不同的点,再和D点构成三角形,求所得三角形与△ABC面积相等的概率是 .

(1)画出△ABC绕点B顺时针方向旋转90°后的图形.
(2)先从E、F、G、H四个点中任意取两个不同的点,再和D点构成三角形,求所得三角形与△ABC面积相等的概率是

考点:作图-旋转变换
专题:
分析:(1)利用旋转的性质得出对应点A′,C′点坐标,进而得出答案;
(2)分别求出各三角形的面积,进而得出与△ABC面积相等的概率.
(2)分别求出各三角形的面积,进而得出与△ABC面积相等的概率.
解答: 解:(1)如图所示:△A′BC′即为所求;
解:(1)如图所示:△A′BC′即为所求;
(2)∵S△ABC=
×3×4=6,
S△DEG=
×4×4=8,
S△FDG=
×3×4=6,
S△HFD=
×1×3=
,
S△HDE=
×3×4=6,
S△FDE=
×4×4=8,
S△HDG=
××3×4=6,
∴所得三角形与△ABC面积相等的概率是:
=
.
故答案为:
.
 解:(1)如图所示:△A′BC′即为所求;
解:(1)如图所示:△A′BC′即为所求;(2)∵S△ABC=
| 1 |
| 2 |
S△DEG=
| 1 |
| 2 |
S△FDG=
| 1 |
| 2 |
S△HFD=
| 1 |
| 2 |
| 3 |
| 2 |
S△HDE=
| 1 |
| 2 |
S△FDE=
| 1 |
| 2 |
S△HDG=
| 1 |
| 2 |
∴所得三角形与△ABC面积相等的概率是:
| 3 |
| 6 |
| 1 |
| 2 |
故答案为:
| 1 |
| 2 |
点评:此题主要考查了三角形面积求法以及图形的旋转变换,得出所有符合题意的三角形面积是解题关键.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目

 如图,在平面直角坐标系中,直线l平行x轴,交y轴于点A,第一象限内的点B在l上,连结OB,动点P满足∠APQ=90°,PQ交x轴于点C.
如图,在平面直角坐标系中,直线l平行x轴,交y轴于点A,第一象限内的点B在l上,连结OB,动点P满足∠APQ=90°,PQ交x轴于点C.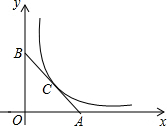 如图,在平面直角坐标系中,点A(4,0)、B(0,4),连接AB,反比例函数y=
如图,在平面直角坐标系中,点A(4,0)、B(0,4),连接AB,反比例函数y=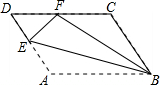 如图,平行四边形ABCD中,点E在AD上,以BE为折痕,把△ABE向上翻折,点A正好落在CD边的点F处,若△FDE的周长为6,△FCB的周长为20,那么CF的长为
如图,平行四边形ABCD中,点E在AD上,以BE为折痕,把△ABE向上翻折,点A正好落在CD边的点F处,若△FDE的周长为6,△FCB的周长为20,那么CF的长为 水仙花是漳州市花,如图,在长为14m,宽为10m的长方形展厅,划出三个形状、大小完全一样的小长方形摆放水仙花,则每个小长方形的周长为
水仙花是漳州市花,如图,在长为14m,宽为10m的长方形展厅,划出三个形状、大小完全一样的小长方形摆放水仙花,则每个小长方形的周长为