Question

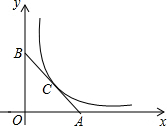如图，在平面直角坐标系中，点A（4，0）、B（0，4），连接AB，反比例函数y=

k

x

（k＞0，x＞0）的图象经过AB的中点C．
（1）求△AOB的面积；
（2）若动点D在反比例函数y=

k

x

（k＞0，x＞0）图象上（点D不与点c重合），以点D为圆心，OD为半径画圆与x轴、y轴分别交于点E、F，连接AF、BE、EF．
①根据上述语句，画出图形，试判断点D是否在EF上？请说明理由；
②猜想AF与BE的位置关系，并说明理由．

Answer 1

考点：反比例函数综合题

专题：

分析：（1）由在平面直角坐标系中，点A（4，0）、B（0，4），即可求得△AOB的面积；
（2）①由∠EOF=90°，根据圆周角定理可得：EF为⊙D 的直径，则可知点D在EF上．
②方法一：过D分别作DP⊥OE，DQ⊥OF，垂足分别为E、F，易求得点C的坐标，即可求得反比例函数的解析式，由反比例函数的性质，易求得S_△AOB=S_△EOF，继而证得△AOF∽△EOB，则可证得AF∥BE；
方法二：首先根据题意可设点D坐标为（a，

4

a

），则OE=2OP=2a，OF=2DP=

8

a

，继而求得直线AF与BE的解析式，即可判定AF与BE的位置关系．

解答：解：（1）∵点A（4，0）、B（0，4），
∴OA=OB=4，
∴S_△AOB=

1

2

OA•OB=

1

2

×4×4=8；

（2）①画图如右所示，点D在EF上．
理由如下：∵∠EOF=90°，
∴EF为⊙D 的直径，
∴点D在EF上．

②AF∥BE．
理由如下：过D分别作DP⊥OE，DQ⊥OF，垂足分别为E、F，
由垂径定理可得：OP=

1

2

OE，OQ=

1

2

OF．
方法一：∴S_△EOF=

1

2

OE•OF=2OP•OQ．
∵A（4，0）、B（0，4），AB的中点为C．
∴C（2，2），
∴反比例函数的解析式为y=

4

x

．
又∵动点D在反比例函数y=

4

x

（x＞0）图象上，
∴OP•OQ=xy=4，
∴S_△EOF=8．
由（1）知，S_△AOB=8，
∴S_△AOB=S_△EOF，
∴OA•OB=OE•OF，
即

OA

OE

=

OF

OB

．
∵∠AOF=∠EOB，
∴△AOF∽△EOB，
∴∠EAO=∠BEO，
∴AF∥BE．

方法二：由A（4，0）、B（0，4）可求得C（2，2），
∴反比例函数的解析式为y=

4

x

．
∵动点D在反比例函数y=

4

x

（x＞0）图象上，
∴可设点D坐标为（a，

4

a

），则OE=2OP=2a，OF=2DP=

8

a

，
∴E（2a，0），F（0，

8

a

），
设直线AF的解析式为y=k₁x+b₁，直线BE的解析式为y=k₂x+b₂，
∵A（4，0），F（0，

8

a

），
∴

4k1+b1=0 b1= 8 a

，
　解得k₁=-

2

a

，
同理可求k₂=-

2

a

，
∴AF∥BE．

点评：此题考查了反比例函数的性质、待定系数法求函数的解析式、相似三角形的判定与性质以及圆周角定理等知识．此题难度较大，综合性较强，注意掌握数形结合思想与方程思想的应用．