题目内容
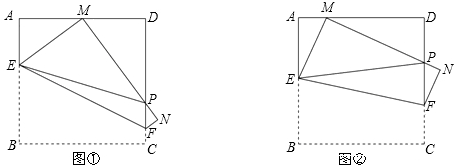
14．
如图，在△ABC中，D、E、F分别是各边的中点，AH是高，∠DHF=50°，∠DAF=50°．
分析 根据直角三角形斜边上的中线等于斜边的一半可得DH=$\frac{1}{2}$AB=AD，从而得到∠1=∠2，同理可证出∠3=∠4，得到∠DHF=∠DAF即可．
解答 
解：如图．∵AH⊥BC于H，
又∵D为AB的中点，
∴DH=$\frac{1}{2}$AB=AD，
∴∠1=∠2，
同理可证：∠3=∠4，
∴∠1+∠3=∠2+∠4，
即∠DHF=∠DAF，
∵∠DHF=50°，
∴∠DAF=50°；
故答案为：50．
点评 此题主要考查了平行四边形的性质与判定，直角三角形斜边上的中线性质，等腰三角形的性质等知识；解决问题的关键是证明∠DHF=∠DAF．
练习册系列答案
相关题目
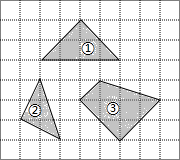如图，在正方形网格中，每个小正方形的边长均相等，网格中三个多边形（分别标记为①，②，③）的顶点均在格点上，被一个多边形覆盖的网格线中，竖直部分线段长度之和记为m，水平部分线段长度之和记为n，则这三个多边形中满足m=n的是②③．
6．下列算式中，结果是$\overrightarrow{AB}$的为（ ）
| A． | $\overrightarrow{CA}-\overrightarrow{CB}$ | B． | $\overrightarrow{CA}-\overrightarrow{BC}$ | C． | $\overrightarrow{AC}-\overrightarrow{CB}$ | D． | $\overrightarrow{AC}-\overrightarrow{BC}$ |