题目内容
9.已知关于x,y的多项式(mx2+nxy-3x+y-1)-(x2-mxy-3x-1)的值与x的取值无关,则(-1)100+m+n|m-n+(-n)m|的值为3.分析 先化简原多项式,根据多项式的值与x无关,可知含x项的系数为0,列方程组解出,求出m、n的值,代入计算即可.
解答 解:(mx2+nxy-3x+y-1)-(x2-mxy-3x-1),
=mx2+nxy-3x+y-1-x2+mxy+3x+1,
=(m-1)x2+(ny-3+my+3)x+y,
∵原多项式的值与x的取值无关,
∴$\left\{\begin{array}{l}{m-1=0}\\{ny+my=0}\end{array}\right.$,
∴$\left\{\begin{array}{l}{m=1}\\{m+n=0}\\{n=-1}\end{array}\right.$,
(-1)100+m+n|m-n+(-n)m|,
=(-1)100×|1+1+1|,
=3.
点评 本题主要考查整式的加法运算,涉及到二次项的定义.根据在多项式中不含哪一项,则哪一项的系数为0,由此建立方程,解方程即可求得待定系数的值.

练习册系列答案
相关题目
4.学校食堂厨房的桌子上整齐地摆放着若干相同规格的碟子,碟子的个数与碟子的高度的关系如下表:
(1)当桌子上放有x(个)碟子时,请写出此时碟子的高度(用含x的式子表示);
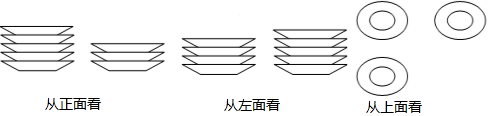
(2)分别从正面、左面、上面三个方向看这些碟子,看到的形状图如图所示,厨房师傅想把它们整齐叠成一摞,求叠成一摞后的高度.
| 碟子的个数 | 1 | 2 | 3 | 4 | … |
| 碟子的高度(单位:cm) | 2 | 2+1.5 | 2+3 | 2+4.5 | … |

(1)当桌子上放有x(个)碟子时,请写出此时碟子的高度(用含x的式子表示);
(2)分别从正面、左面、上面三个方向看这些碟子,看到的形状图如图所示,厨房师傅想把它们整齐叠成一摞,求叠成一摞后的高度.
1.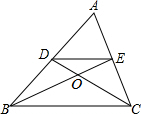 如图,在△ABC中,两条中线BE,CD相交于点O,则S△DOE:S△COB等于( )
如图,在△ABC中,两条中线BE,CD相交于点O,则S△DOE:S△COB等于( )
 如图,在△ABC中,两条中线BE,CD相交于点O,则S△DOE:S△COB等于( )
如图,在△ABC中,两条中线BE,CD相交于点O,则S△DOE:S△COB等于( )| A. | 1:2 | B. | 1:3 | C. | 1:4 | D. | 2:3 |
18.不等式3x-1≤2(x+2)的正整数解有几个( )
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |

 如图,在△ABC中,D、E、F分别是各边的中点,AH是高,∠DHF=50°,∠DAF=50°.
如图,在△ABC中,D、E、F分别是各边的中点,AH是高,∠DHF=50°,∠DAF=50°.