题目内容
11.计算:(1)3x3•x9+x2•x10-2x•x3•x8
(2)(-a2)3+(-a3)2-a2•a3
(3)(p-q)4•(q-p)3•(p-q)2
(4)(-2x2)3+x2•x4-(-3x3)2
(5)已知am=2,an=4,求a3m+2n的值.
(6)已知a2n=4,b2n=9,求an•bn的值.
分析 (1)根据同底数幂的乘法、合并同类项进行计算即可;
(2)根据幂的乘方、合并同类项进行计算即可;
(3)根据同底数幂的乘法进行计算即可;
(4)根据同底数幂的乘法、积的乘方、合并同类项进行计算即可;
(5)根据积的乘方和幂的乘方的逆运算进行计算即可;
(6)根据积的乘方和幂的乘方的逆运算进行计算即可.
解答 解:(1)原式=3x12+x12-2x12
=2x12;
(2)原式=-a6+a6-a5
=-a5;
(3)原式=(p-q)4•[-(p-q)3]•(p-q)2
=-(p-q)9
=(q-p)9;
(4)原式=-8x6+x6-9x6
=-16x6;
(5)∵am=2,an=4,
∴a3m+2n=(am)3•(an)2
=8×16,
=128;
(6)∵a2n=4,b2n=9,
∴an=±2,bn=±3,
∴an•bn=±6.
点评 本题考查了整式的混合运算,熟练掌握同底数幂的乘法、积的乘方、合并同类项、幂的乘方以及逆运算是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
13.-10+3的结果是( )
| A. | -7 | B. | 7 | C. | -13 | D. | 13 |
19.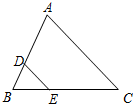 如图,△ABC中,若DE∥AC,则下列等式不成立的是( )
如图,△ABC中,若DE∥AC,则下列等式不成立的是( )
 如图,△ABC中,若DE∥AC,则下列等式不成立的是( )
如图,△ABC中,若DE∥AC,则下列等式不成立的是( )| A. | $\frac{AD}{BD}=\frac{CE}{EB}$ | B. | $\frac{AD}{AB}=\frac{CE}{CB}$ | C. | $\frac{BD}{BA}=\frac{BE}{BC}$ | D. | $\frac{DE}{AC}=\frac{BE}{EC}$ |
 如图,抛物线y=-$\frac{5}{4}$x2+bx+c与y轴交于点A(0,1),过点A的直线与抛物线交于另一点B(3,$\frac{5}{2}$),过点B作BC⊥x轴,垂足为C.
如图,抛物线y=-$\frac{5}{4}$x2+bx+c与y轴交于点A(0,1),过点A的直线与抛物线交于另一点B(3,$\frac{5}{2}$),过点B作BC⊥x轴,垂足为C.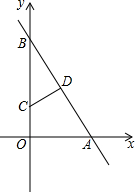 如图,在平面直角坐标系中,直线与x轴、y轴分别交于点A(6,0)、点B(0,6$\sqrt{3}$),点D是线段AB的中点,点C(0,2$\sqrt{3}$),点E为x轴上一动点.
如图,在平面直角坐标系中,直线与x轴、y轴分别交于点A(6,0)、点B(0,6$\sqrt{3}$),点D是线段AB的中点,点C(0,2$\sqrt{3}$),点E为x轴上一动点.