题目内容
1.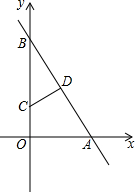 如图,在平面直角坐标系中,直线与x轴、y轴分别交于点A(6,0)、点B(0,6$\sqrt{3}$),点D是线段AB的中点,点C(0,2$\sqrt{3}$),点E为x轴上一动点.
如图,在平面直角坐标系中,直线与x轴、y轴分别交于点A(6,0)、点B(0,6$\sqrt{3}$),点D是线段AB的中点,点C(0,2$\sqrt{3}$),点E为x轴上一动点.(1)求直线AB的表达式,并直接写出点D的坐标;
(2)联结CE、DE,以CE、DE为边作?CEDF,?CEDF的顶点F恰好落在y轴上,求点F的坐标;
(3)设点M是直线y=x+4$\sqrt{3}$上一点,若以C、D、E、M为顶点的四边形为平行四边形,请直接写出所有符合条件的点M的坐标.
分析 (1)利用待定系数法求出直线AB的表达式.
(2)由于以CD,DE为边的四边形为平行四边形,且点C、F都在y轴上,所以利用DE平行且相等于CF即可.
(3)①CD为平行四边形的对角线EM也是这个平行四边形的对角线,CD,EM平行四边形的对角线的交点是同一个点,把点E,M的坐标设出,利用中点坐标的确定方法,求出CD的中点和EM得中点,是同一个点,即可,②CD为以C、D、E、M为顶点的四边形为平行四边形的边,利用CD∥EM且CD=EM,即可求出.
解答 解:(1)设直线AB的表达式为y=kx+b,
∵直线AB与x轴,y轴分别相交于点A(6,0)、B(0,6$\sqrt{3}$),
∴6k+b=0,b=6$\sqrt{3}$,
∴k=-$\sqrt{3}$,
即:直线AB的表达式为y=-$\sqrt{3}$x+6$\sqrt{3}$.
(2)如图,
∵点D是AB的中点,A(6,0),B(0,6$\sqrt{3}$)
∴D(3,3$\sqrt{3}$),
∵C(0,2$\sqrt{3}$),
∵以CD、DE为边的平行四边形交x轴于E,交y轴于F,
∴E(3,0),
∴DE=3$\sqrt{3}$,
∴CF=3$\sqrt{3}$,
∴F(0,-$\sqrt{3}$).
(3)第一种情况:CD为平行四边形的对角线,
∵D(3,3$\sqrt{3}$),C(0,2$\sqrt{3}$),
∴CD的中点坐标为($\frac{3}{2}$,$\frac{5\sqrt{3}}{2}$),
∵点M在直线y=x+4$\sqrt{3}$的图象上,
设M(m,m+4$\sqrt{3}$),E(x,y),
∴ME中点坐标为($\frac{m+x}{2}$,$\frac{m+4\sqrt{3}+y}{2}$),
∵CD,ME为平行四边形的对角线,
∴$\frac{3}{2}$=$\frac{m+x}{2}$,$\frac{5\sqrt{3}}{2}$=$\frac{m+4\sqrt{3}+y}{2}$,
∴x=3-m,y=$\sqrt{3}$-m,
∵点E在x轴上,
∴y=0,
∴m=$\sqrt{3}$,
即M($\sqrt{3}$,5$\sqrt{3}$),E(3-$\sqrt{3}$,0),
第二种情况:CD为平行四边形的边,则EM也为边,
即CD∥EM,CD=EM,
∵点C(0,2$\sqrt{3}$)、点D(3,3$\sqrt{3}$),
∴CD=2$\sqrt{3}$,
直线CD的表达式为y=$\frac{\sqrt{3}}{3}$x+2$\sqrt{3}$,
∴直线EM的表达式可设为为y=$\frac{\sqrt{3}}{3}$x+b,
∴E(-$\sqrt{3}$b,0),
设M(m,m+4$\sqrt{3}$),
∴EM2=(m+$\sqrt{3}$b)2+(m+4$\sqrt{3}$)2=CD2=12①
点M在直线EM的图象上,
∴m+4$\sqrt{3}$=$\frac{\sqrt{3}}{3}m+b$②
由①②有m=-3$\sqrt{3}$或m=-5$\sqrt{3}$,
M1(-3$\sqrt{3}$,$\sqrt{3}$),E1(-3-3$\sqrt{3}$,0)
M2(-5$\sqrt{3}$,-$\sqrt{3}$),E2(3-5$\sqrt{3}$,0)
故符合条件的点的坐标为 M1(-3$\sqrt{3}$,$\sqrt{3}$),E1(-3-3$\sqrt{3}$,0)
M2(-5$\sqrt{3}$,-$\sqrt{3}$),E2(3-5$\sqrt{3}$,0)
M3($\sqrt{3}$,5$\sqrt{3}$),E2(3-$\sqrt{3}$,0).
点评 本题是一次函数综合题,主要考查了一次函数表达式的确定以及一次函数和平行四边形的判定的综合运用.用到的知识点比较多,如确定直线的表达式,平行四边形的性质,线段的中点坐标的确定,本题的关键是线段的中点坐标的确定和两点之间的距离的计算方法的确定,如EM2=(m+$\sqrt{3}$b)2+(m+4$\sqrt{3}$)2=CD2=12.

 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案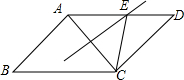 如图,平行四边形ABCD中,AB=6,BC=8,AC的垂直平分线交AD于E,则三角形CDE的周长是( )
如图,平行四边形ABCD中,AB=6,BC=8,AC的垂直平分线交AD于E,则三角形CDE的周长是( )| A. | 6 | B. | 8 | C. | 14 | D. | 16 |
| A. | 有两个相等的实数根 | B. | 只有一个实数根 | ||
| C. | 没有实数根 | D. | 有两个不相等的实数根 |
| 捐款数(元) | 10 | 20 | 30 | 40 | 50 |
| 捐款人数(人) | 8 | 17 | 16 | 2 | 2 |
