题目内容
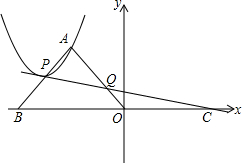 如图,在△AOB中,∠OAB=90°,OA=AB,点B的坐标为(-4,0),过点C(4,0)作直线l交AB于P,交AO于Q,以P为顶点的抛物线经过点A,当△APQ和△COQ的面积相等时,则抛物线解析式为
如图,在△AOB中,∠OAB=90°,OA=AB,点B的坐标为(-4,0),过点C(4,0)作直线l交AB于P,交AO于Q,以P为顶点的抛物线经过点A,当△APQ和△COQ的面积相等时,则抛物线解析式为考点:二次函数综合题
专题:
分析:过P点作PE⊥BC于点E,过A点作AF⊥BO于点F,根据等腰直角三角形的性质可得A(-2,2),再根据△APQ和△COQ的面积相等可得P点纵坐标为1.根据待定系数法可得直线AB的解析式,从而得到P点坐标,再根据抛物线的顶点式,根据待定系数法可得抛物线解析式.
解答: 解:过P点作PE⊥BC于点E,过A点作AF⊥BO于点F.
解:过P点作PE⊥BC于点E,过A点作AF⊥BO于点F.
∵B(-4,0),C(4,0),
∴BC=4-(-4)=8.
∵OA=AB,AF⊥BO于点F,
∴F为OB中点,
∵∠OAB=90°,
∴AF=
OB=2,
∴A(-2,2),
∴S△ABO=
BO•AF=
×4×2=4.
∵S△ABO=S△APQ+S四边形PQBO,S△APQ=S△COQ,
∴S△ABO=S△COQ+S四边形PQBO=S△BCP=4.
∵S△BCP=
BC•PE=
×8•PE=4PE=4,
∴PE=1,即P点纵坐标为1.
设直线AB的解析式为y=kx+b,
∵A(-2,2),B(-4,0),
∴
,
解得
,
∴y=x+4,
当y=1时,x+4=1,
解得x=-3,
∴P(-3,1).
设所求抛物线的解析式为y=a(x+3)2+1,
将A(-2,2)代入,得a(-2+3)2+1=2,
解得a=1,
∴抛物线解析式为y=(x+3)2+1,即y=x2+6x+10.
 解:过P点作PE⊥BC于点E,过A点作AF⊥BO于点F.
解:过P点作PE⊥BC于点E,过A点作AF⊥BO于点F.∵B(-4,0),C(4,0),
∴BC=4-(-4)=8.
∵OA=AB,AF⊥BO于点F,
∴F为OB中点,
∵∠OAB=90°,
∴AF=
| 1 |
| 2 |
∴A(-2,2),
∴S△ABO=
| 1 |
| 2 |
| 1 |
| 2 |
∵S△ABO=S△APQ+S四边形PQBO,S△APQ=S△COQ,
∴S△ABO=S△COQ+S四边形PQBO=S△BCP=4.
∵S△BCP=
| 1 |
| 2 |
| 1 |
| 2 |
∴PE=1,即P点纵坐标为1.
设直线AB的解析式为y=kx+b,
∵A(-2,2),B(-4,0),
∴
|
解得
|
∴y=x+4,
当y=1时,x+4=1,
解得x=-3,
∴P(-3,1).
设所求抛物线的解析式为y=a(x+3)2+1,
将A(-2,2)代入,得a(-2+3)2+1=2,
解得a=1,
∴抛物线解析式为y=(x+3)2+1,即y=x2+6x+10.
点评:考查了二次函数综合题,涉及的知识点有:等腰直角三角形的性质,三角形的面积计算,待定系数法求直线的解析式,抛物线的顶点式,以及待定系数法求抛物线解析式,综合性较强,难度中等.

练习册系列答案
相关题目
 如图,在矩形ABCD中,把∠D沿AE折叠,使点D落在BC边上的点F处,已知∠BAF=60°,则∠DAE的度数是( )
如图,在矩形ABCD中,把∠D沿AE折叠,使点D落在BC边上的点F处,已知∠BAF=60°,则∠DAE的度数是( )| A、15° | B、30° |
| C、45° | D、60° |
在下列式子中,正确的是( )
A、
| ||||||
B、-
| ||||||
C、
| ||||||
D、
|
 一次函数y=kx+b的图象如图,当y<0时,x的取值范围是
一次函数y=kx+b的图象如图,当y<0时,x的取值范围是 如图,点C在直线MN上,AC⊥BC于点C,∠1=65°,则∠2=
如图,点C在直线MN上,AC⊥BC于点C,∠1=65°,则∠2= 如图,已知AD是△ABC的角平分线,AD⊥BC,则△ABC是
如图,已知AD是△ABC的角平分线,AD⊥BC,则△ABC是 如图,四边形ABCD为正方形,∠APC=90°,若AB=10,PD=6
如图,四边形ABCD为正方形,∠APC=90°,若AB=10,PD=6