题目内容
 如图,已知AD是△ABC的角平分线,AD⊥BC,则△ABC是
如图,已知AD是△ABC的角平分线,AD⊥BC,则△ABC是考点:等腰三角形的判定
专题:
分析:根据角平分线的定义可得∠BAD=∠CAD,根据垂直的定义可得∠ADB=∠ADC=90°,然后利用“角边角”证明△ABD和△ACD全等,根据全等三角形对应边相等可得AB=AC,从而判断出△ABC是等腰三角形.
解答:解:∵AD是△ABC的角平分线,
∴∠BAD=∠CAD,
∵AD⊥BC,
∴∠ADB=∠ADC=90°,
在△ABD和△ACD中,
,
∴△ABD≌△ACD(ASA),
∴AB=AC,
∴△ABC是等腰三角形.
故答案为:等腰.
∴∠BAD=∠CAD,
∵AD⊥BC,
∴∠ADB=∠ADC=90°,
在△ABD和△ACD中,
|
∴△ABD≌△ACD(ASA),
∴AB=AC,
∴△ABC是等腰三角形.
故答案为:等腰.
点评:本题考查了等腰三角形的判定,全等三角形的判定与性质,确定并证明出全等三角形是解题的关键.

练习册系列答案
相关题目
 如图几何体的左视图是( )
如图几何体的左视图是( )A、 |
B、 |
C、 |
D、 |
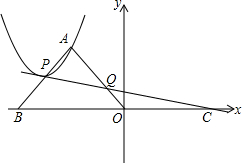 如图,在△AOB中,∠OAB=90°,OA=AB,点B的坐标为(-4,0),过点C(4,0)作直线l交AB于P,交AO于Q,以P为顶点的抛物线经过点A,当△APQ和△COQ的面积相等时,则抛物线解析式为
如图,在△AOB中,∠OAB=90°,OA=AB,点B的坐标为(-4,0),过点C(4,0)作直线l交AB于P,交AO于Q,以P为顶点的抛物线经过点A,当△APQ和△COQ的面积相等时,则抛物线解析式为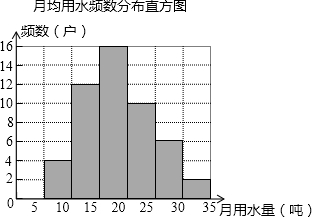 每年的3月22日被联合国为世界水日,旨在唤起公众的水意识,加强水资源保护.为响应号召,小聪同学随机调查了某小区部分家庭月均用水量并将调查数据进行整理,绘制频数分布直方图如图,则被抽查的用户中月均用水落在20~25(吨)的频率是( )
每年的3月22日被联合国为世界水日,旨在唤起公众的水意识,加强水资源保护.为响应号召,小聪同学随机调查了某小区部分家庭月均用水量并将调查数据进行整理,绘制频数分布直方图如图,则被抽查的用户中月均用水落在20~25(吨)的频率是( )