题目内容
 如图,四边形ABCD为正方形,∠APC=90°,若AB=10,PD=6
如图,四边形ABCD为正方形,∠APC=90°,若AB=10,PD=6| 5 |
考点:全等三角形的判定与性质,勾股定理,等腰直角三角形,正方形的性质
专题:计算题
分析:如图,延长PA至E,使得AE=PC,作DH⊥EP,利用SAS证明△EAD≌△PCD,根据全等三角形对应边相等,对应角相等得到DE=DP,∠EDA=∠PDC,利用等式的性质及正方形的性质得到∠EDP为直角,确定出△EDP为等腰直角三角形,进而得到三角形HDP为等腰直角三角形,根据DP的长求出DH的长,在直角三角形ADH中,利用勾股定理求出AH的长,利用锐角三角函数定义求出tan∠PAD的值即可.
解答: 解:如图,延长PA至E,使得AE=PC,作DH⊥EP,
解:如图,延长PA至E,使得AE=PC,作DH⊥EP,
∵∠APC=∠ADC=90°,
∴A,P,C,D四点共圆,
∴∠DAP+∠DCP=180°,
∵∠DAP+∠DAE=180°,
∴∠DCP=∠DAE,
在△EAD和△PCD中,
,
∴△EAD≌△PCD(SAS),
∴DE=DP,∠EDA=∠PDC,
∵∠ADP+∠PDC=90°,
∴∠EDA+∠ADP=90°,即∠EDP=90°,
∴△EDP为等腰直角三角形,
∴∠DPH=45°,即△DHP为等腰直角三角形,
∴DH=
DP=3
,
在Rt△ADH中,AD=10,DH=3
,
根据勾股定理得:AH=
=
,
∴tan∠PAD=
=
=3.
故答案为:3.
 解:如图,延长PA至E,使得AE=PC,作DH⊥EP,
解:如图,延长PA至E,使得AE=PC,作DH⊥EP,∵∠APC=∠ADC=90°,
∴A,P,C,D四点共圆,
∴∠DAP+∠DCP=180°,
∵∠DAP+∠DAE=180°,
∴∠DCP=∠DAE,
在△EAD和△PCD中,
|
∴△EAD≌△PCD(SAS),
∴DE=DP,∠EDA=∠PDC,
∵∠ADP+∠PDC=90°,
∴∠EDA+∠ADP=90°,即∠EDP=90°,
∴△EDP为等腰直角三角形,
∴∠DPH=45°,即△DHP为等腰直角三角形,
∴DH=
| ||
| 2 |
| 10 |
在Rt△ADH中,AD=10,DH=3
| 10 |
根据勾股定理得:AH=
102-(3
|
| 10 |
∴tan∠PAD=
| DH |
| AH |
3
| ||
|
故答案为:3.
点评:此题考查了全等三角形的判定与性质,等腰直角三角形的判定与性质,正方形的性质,以及勾股定理,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
相关题目
太阳的半径约为696 000千米,这个数保留2个有效数字得到的数是( )
| A、70 |
| B、700000 |
| C、7×105 |
| D、7.0×105 |
 如图所示,在△ABC中,∠ACB=90°,AC=12,BC=5,AM=AC,BN=BC,则MN的长为
如图所示,在△ABC中,∠ACB=90°,AC=12,BC=5,AM=AC,BN=BC,则MN的长为 把一张长方形纸片(矩形ABCD)按如图方式折叠,使顶点B和点D重合,折痕为EF,若AB=6,BC=8,则折痕EF的长为
把一张长方形纸片(矩形ABCD)按如图方式折叠,使顶点B和点D重合,折痕为EF,若AB=6,BC=8,则折痕EF的长为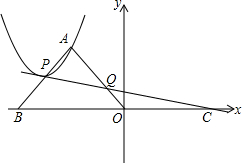 如图,在△AOB中,∠OAB=90°,OA=AB,点B的坐标为(-4,0),过点C(4,0)作直线l交AB于P,交AO于Q,以P为顶点的抛物线经过点A,当△APQ和△COQ的面积相等时,则抛物线解析式为
如图,在△AOB中,∠OAB=90°,OA=AB,点B的坐标为(-4,0),过点C(4,0)作直线l交AB于P,交AO于Q,以P为顶点的抛物线经过点A,当△APQ和△COQ的面积相等时,则抛物线解析式为 如图,已知点A(3,n)在反比例函数y=
如图,已知点A(3,n)在反比例函数y=