题目内容
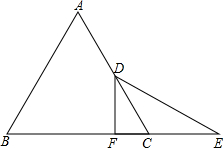 如图,△ABC是等边三角形,D是AC的中点,延长BC至E,CE=CD,DF⊥BC于F,求证:BF=EF.
如图,△ABC是等边三角形,D是AC的中点,延长BC至E,CE=CD,DF⊥BC于F,求证:BF=EF.考点:等边三角形的性质
专题:证明题
分析:先根据△ABC是等边三角形,BD⊥AC可知∠DBE=30°,∠ACB=60°,再根据CE=CD可知∠CDE=∠E,由三角形外角的性质可知∠ACB=∠E+∠CDE=60°,故∠E=30°,故可得出∠E=∠DBE=30°,故BD=DE,再根据DF⊥BE可知BF=EF.
解答: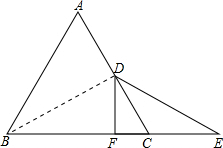 证明:连接BD,
证明:连接BD,
∵△ABC是等边三角形,BD⊥AC,
∴∠DBE=30°,∠ACB=60°,
∵CE=CD,
∴∠CDE=∠E,
∵∠ACB是△CDE的外角,
∴∠ACB=∠E+∠CDE=60°,
∴∠E=30°,
∴∠E=∠DBE=30°,
∴BD=DE,
∴△BDE是等腰三角形,
∵DF⊥BE,
∴BF=EF.
 证明:连接BD,
证明:连接BD,∵△ABC是等边三角形,BD⊥AC,
∴∠DBE=30°,∠ACB=60°,
∵CE=CD,
∴∠CDE=∠E,
∵∠ACB是△CDE的外角,
∴∠ACB=∠E+∠CDE=60°,
∴∠E=30°,
∴∠E=∠DBE=30°,
∴BD=DE,
∴△BDE是等腰三角形,
∵DF⊥BE,
∴BF=EF.
点评:本题考查的是等边三角形的性质及三角形外角的性质,根据题意得出△BDE是等腰三角形是解答此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
一列火车匀速前进,从它进入300米长的隧道到完全通过共需20秒钟,又知隧道顶部一束固定的灯光垂直照射列车10秒钟,求这列火车的长度.在这个问题中,下列说法正确的是( )
| A、火车走300米路程用时20秒 |
| B、火车10秒钟走的路程等于隧道长与车身长的差 |
| C、火车20秒钟走的路程等于车身长和隧道长的和 |
| D、以上都不对 |
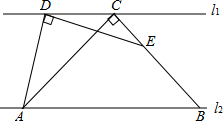 已知,如图,l1∥l2,AC=BC,∠ADE=90°,∠ACB=90°,求证:AD=DE.
已知,如图,l1∥l2,AC=BC,∠ADE=90°,∠ACB=90°,求证:AD=DE.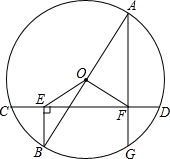 已知,AB为圆O的直径,CD是弦,BE⊥CD于E,AF⊥CD于F,连接OE,OF,求证:
已知,AB为圆O的直径,CD是弦,BE⊥CD于E,AF⊥CD于F,连接OE,OF,求证: