题目内容
已知在△ABC中,AB=
,AC=
,∠B=45°,这样的△ABC有几个?请画出来并求∠ACB的度数.
| 3 |
| 2 |
考点:勾股定理
专题:分类讨论
分析:分△ABC是钝角三角形和锐角三角形两种情况讨论可得∠ACB的度数.
解答:解:如图所示:

如图1,过A点作AD⊥BC交BC的延长线于D.
∵AB=
,∠B=45°,
∴AD=
,
∵AC=
,
在Rt△ADC中,sin∠ACD=
=
,
∴∠ACD=60°,
∴∠ACB=120°;
如图2,过A点作AD⊥BC交BC于D.
∵AB=
,∠B=45°,
∴AD=
,
在Rt△ADC中,sin∠ACD=
=
,
∴∠ACB=60°.
综上所述,这样的△ABC有2个,∠ACB的度数是120°或60°.

如图1,过A点作AD⊥BC交BC的延长线于D.
∵AB=
| 3 |
∴AD=
| ||
| 2 |
∵AC=
| 2 |
在Rt△ADC中,sin∠ACD=
| AD |
| AC |
| ||
| 2 |
∴∠ACD=60°,
∴∠ACB=120°;
如图2,过A点作AD⊥BC交BC于D.
∵AB=
| 3 |
∴AD=
| ||
| 2 |
在Rt△ADC中,sin∠ACD=
| AD |
| AC |
| ||
| 2 |
∴∠ACB=60°.
综上所述,这样的△ABC有2个,∠ACB的度数是120°或60°.
点评:考查了勾股定理:在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方.注意分类思想的运用.

练习册系列答案
相关题目
数2和8的比例中项是( )
| A、±4 | B、±5 | C、4 | D、5 |

 如图,已知PA、PB为⊙O的切线,切点分别为点A、B,∠P=60°,AB=4
如图,已知PA、PB为⊙O的切线,切点分别为点A、B,∠P=60°,AB=4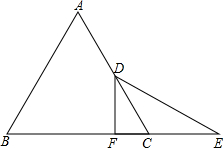 如图,△ABC是等边三角形,D是AC的中点,延长BC至E,CE=CD,DF⊥BC于F,求证:BF=EF.
如图,△ABC是等边三角形,D是AC的中点,延长BC至E,CE=CD,DF⊥BC于F,求证:BF=EF.