题目内容
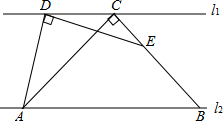 已知,如图,l1∥l2,AC=BC,∠ADE=90°,∠ACB=90°,求证:AD=DE.
已知,如图,l1∥l2,AC=BC,∠ADE=90°,∠ACB=90°,求证:AD=DE.考点:全等三角形的判定与性质
专题:证明题
分析:过D作DF⊥DC,交AC于点F,利用同角的余角相等得到一对角相等,再由三角形ABC为等腰直角三角形且l1∥l2,得到∠DCF=∠CAB=45°,即三角形DCF为等腰直角三角形,进而得到DF=DC,利用邻补角定义及等式性质得到一对角相等,利用ASA得到三角形ADF与三角形EDC全等,利用全等三角形的对应边相等即可得证.
解答: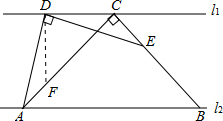 解:过D作DF⊥DC,交AC于点F,
解:过D作DF⊥DC,交AC于点F,
∵∠ADF+∠FDE=90°,∠CDE+∠FDE=90°,
∴∠ADF=∠CDE,
∵△ABC为等腰直角三角形,且l1∥l2,
∴∠DCF=∠CAB=45°,
∴△DCF为等腰直角三角形,
∴DF=DC,∠AFD=∠ECD=135°,
在△ADF和△EDC中,
,
∴△ADF≌△EDC(ASA),
∴AD=DE.
 解:过D作DF⊥DC,交AC于点F,
解:过D作DF⊥DC,交AC于点F,∵∠ADF+∠FDE=90°,∠CDE+∠FDE=90°,
∴∠ADF=∠CDE,
∵△ABC为等腰直角三角形,且l1∥l2,
∴∠DCF=∠CAB=45°,
∴△DCF为等腰直角三角形,
∴DF=DC,∠AFD=∠ECD=135°,
在△ADF和△EDC中,
|
∴△ADF≌△EDC(ASA),
∴AD=DE.
点评:此题考查了全等三角形的判定与性质,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
相关题目
下列说法正确的是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
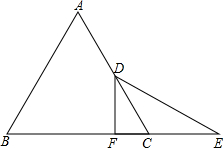 如图,△ABC是等边三角形,D是AC的中点,延长BC至E,CE=CD,DF⊥BC于F,求证:BF=EF.
如图,△ABC是等边三角形,D是AC的中点,延长BC至E,CE=CD,DF⊥BC于F,求证:BF=EF. 如图所示,已知△ABC中的∠ACB的外角平分线CD与∠ABC的平分线BD交于点D,过D作DE∥BC交AB于E,交AC于F,则有EF=BE-CF;试说明理由.
如图所示,已知△ABC中的∠ACB的外角平分线CD与∠ABC的平分线BD交于点D,过D作DE∥BC交AB于E,交AC于F,则有EF=BE-CF;试说明理由.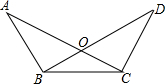 如图所示,已知△ABC≌△DCB,∠A=32°,∠BCD=115°,求∠BOC.
如图所示,已知△ABC≌△DCB,∠A=32°,∠BCD=115°,求∠BOC.