题目内容
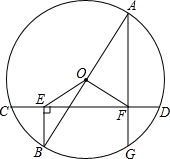 已知,AB为圆O的直径,CD是弦,BE⊥CD于E,AF⊥CD于F,连接OE,OF,求证:
已知,AB为圆O的直径,CD是弦,BE⊥CD于E,AF⊥CD于F,连接OE,OF,求证:(1)OE=OF;
(2)CE=DF.
考点:垂径定理,矩形的判定与性质,圆周角定理
专题:证明题
分析:(1)连接OC、OD、OG,作OH⊥BG于H,交CD于M,根据已知条件证得四边形BGFE是矩形,得出BG=EF,BG∥EF,根据垂径定理证得BH=GH,EF⊥OH,进而证得四边形BHME和四边形GHMF也是矩形,从而证得ME=BH=GH=MF,根据线段的垂直平分线的性质即可证得OE=OF.
(2)根据垂径定理得出CM=DM,由(1)已经证得ME=MF,根据等量减等量还是等量即可证得.
(2)根据垂径定理得出CM=DM,由(1)已经证得ME=MF,根据等量减等量还是等量即可证得.
解答: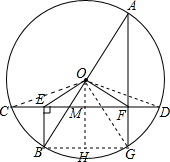 (1)证明:连接OC、OD、OG,作OH⊥BG于H,交CD于M,
(1)证明:连接OC、OD、OG,作OH⊥BG于H,交CD于M,
∵AB为圆O的直径,BE⊥CD于E,AF⊥CD于F,
∴∠BGF=90°,
∴四边形BGFE是矩形,
∴BG=EF,BG∥EF,
∵OH⊥BG,
∴BH=GH,EF⊥OH,
∴四边形BHME和四边形GHMF也是矩形,
∴ME=BH=GH=MF,
∴OE=OF.
(2)证明:∵OM⊥CD,
∴CM=DM,
∵ME=MF,
∴CM-ME=DM-MF,
即CE=DF.
 (1)证明:连接OC、OD、OG,作OH⊥BG于H,交CD于M,
(1)证明:连接OC、OD、OG,作OH⊥BG于H,交CD于M,∵AB为圆O的直径,BE⊥CD于E,AF⊥CD于F,
∴∠BGF=90°,
∴四边形BGFE是矩形,
∴BG=EF,BG∥EF,
∵OH⊥BG,
∴BH=GH,EF⊥OH,
∴四边形BHME和四边形GHMF也是矩形,
∴ME=BH=GH=MF,
∴OE=OF.
(2)证明:∵OM⊥CD,
∴CM=DM,
∵ME=MF,
∴CM-ME=DM-MF,
即CE=DF.
点评:本题考查了垂径定理和矩形的性质以及线段的垂直平分线的性质等,垂径定理的应用是解题的关键.

练习册系列答案
 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案
相关题目

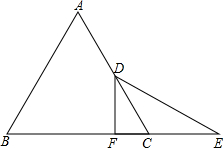 如图,△ABC是等边三角形,D是AC的中点,延长BC至E,CE=CD,DF⊥BC于F,求证:BF=EF.
如图,△ABC是等边三角形,D是AC的中点,延长BC至E,CE=CD,DF⊥BC于F,求证:BF=EF.
 如图所示,已知△ABC中的∠ACB的外角平分线CD与∠ABC的平分线BD交于点D,过D作DE∥BC交AB于E,交AC于F,则有EF=BE-CF;试说明理由.
如图所示,已知△ABC中的∠ACB的外角平分线CD与∠ABC的平分线BD交于点D,过D作DE∥BC交AB于E,交AC于F,则有EF=BE-CF;试说明理由. 如图:
如图: