题目内容
在正方形ABCD中,点E、F分别在AB、BC上,且BE=CF,试说明CE与DF的关系.
考点:正方形的性质
专题:
分析:BE=CF,结合正方形的性质可证明Rt△BEC≌Rt△CFD,再结合角之间的关系可知CE=DF,且CE⊥DF.
解答:解:CE=DF且CE⊥DF,理由如下:
由正方形的性质可知:BC=CD,∠B=∠FCD,
在△BEC和△CFD中
∴Rt△BEC≌Rt△CFD(SAS),
∴CE=DF,∠FDC=∠ECF,
∵∠ECF+∠DCE=90°,
∴∠FDC+∠DCE=90°,
不妨设CE和DF相交于点O,则∠DOC=90°,
即CE⊥DF.
由正方形的性质可知:BC=CD,∠B=∠FCD,
在△BEC和△CFD中
|
∴Rt△BEC≌Rt△CFD(SAS),
∴CE=DF,∠FDC=∠ECF,
∵∠ECF+∠DCE=90°,
∴∠FDC+∠DCE=90°,
不妨设CE和DF相交于点O,则∠DOC=90°,
即CE⊥DF.
点评:本题主要考查正方形的性质的运用,解题的关键是把CE和DF放到两个三角形中,证明三角形全等,从而找到它们之间的关系,注意关系包括两方面的,即数量上和位置上的.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
分别有下列几组数据:①6、8、10 ②12、13、5 ③17、8、15 ④4、11、9,其中能构成直角三形的有( )
| A、4组 | B、3组 | C、2组 | D、1组 |
在
、-
、-
、
中,最简二次根式的个数是( )
| 16x3 |
| ||
| 3 |
| 0.5 |
|
| A、1 | B、2 | C、3 | D、4 |

 如图,已知PA、PB为⊙O的切线,切点分别为点A、B,∠P=60°,AB=4
如图,已知PA、PB为⊙O的切线,切点分别为点A、B,∠P=60°,AB=4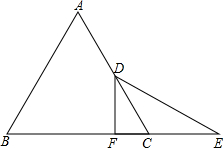 如图,△ABC是等边三角形,D是AC的中点,延长BC至E,CE=CD,DF⊥BC于F,求证:BF=EF.
如图,△ABC是等边三角形,D是AC的中点,延长BC至E,CE=CD,DF⊥BC于F,求证:BF=EF. 如图:
如图: