题目内容
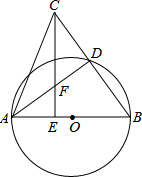 如图所示,在△ABC中,AB=AC,AE=
如图所示,在△ABC中,AB=AC,AE=| 1 |
| 3 |
考点:圆周角定理,三角形中位线定理
专题:证明题
分析:作DH∥CE,交AB于H,先由AB为⊙O直径,根据圆周角定理得出AD⊥BC,根据等腰三角形三线合一的性质得出CD=BD,那么由三角形中位线定理得到BH=EH,又AE=
AB,于是得出AE=EH,再由EF∥DH,即可证明AF=FD.
| 1 |
| 3 |
解答: 证明:作DH∥CE,交AB于H.
证明:作DH∥CE,交AB于H.
∵AB为⊙O直径,
∴AD⊥BC,
∵AB=AC,
∴CD=BD,
∴BH=EH,
又AE=
AB,
∴AE=EH,
∵EF∥DH,
∴AF=FD.
 证明:作DH∥CE,交AB于H.
证明:作DH∥CE,交AB于H.∵AB为⊙O直径,
∴AD⊥BC,
∵AB=AC,
∴CD=BD,
∴BH=EH,
又AE=
| 1 |
| 3 |
∴AE=EH,
∵EF∥DH,
∴AF=FD.
点评:本题考查了圆周角定理,等腰三角形的性质,三角形中位线定理,难度适中.准确作出辅助线是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
计算:
-
的结果为( )
| x2-y2 |
| xy |
| xy-y2 |
| xy-x2 |
A、
| ||
B、
| ||
| C、x2 | ||
| D、x-2y |
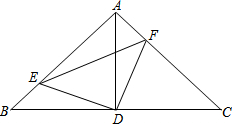 如图,在Rt△ABC中,∠BAC=90°,点D为BC中点,点E、F分别为AB、AC上的点,且ED⊥FD.以线段BE、EF、FC为边能否构成一个三角形?若能,请判断此三角形的形状.
如图,在Rt△ABC中,∠BAC=90°,点D为BC中点,点E、F分别为AB、AC上的点,且ED⊥FD.以线段BE、EF、FC为边能否构成一个三角形?若能,请判断此三角形的形状.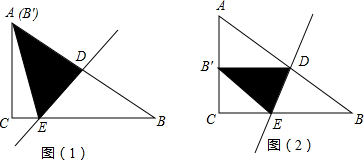
 如图,圆的两弦的延长线交圆外于点P,若PC=4,CD=3,A为PB中点,求PB的长.
如图,圆的两弦的延长线交圆外于点P,若PC=4,CD=3,A为PB中点,求PB的长.