题目内容
 如图,已知直角扇形AOB的半径OA=2cm,以OB为直径在扇形内作半圆M,过点M引MP∥AO交
如图,已知直角扇形AOB的半径OA=2cm,以OB为直径在扇形内作半圆M,过点M引MP∥AO交 |
| AB |
 |
| AB |
考点:扇形面积的计算
专题:
分析:要求的阴影部分的面积显然是不规则图形的面积,不可能直接用公式,只有用“割补法”,连结OP,根据S阴影=S扇形AOB-S扇形BMQ-S△MOP-S扇形OAP即可得出结论.
解答: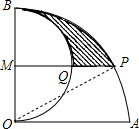 解:如图,连结OP.
解:如图,连结OP.
∵AO⊥OB,MP∥OA,
∴MP⊥OB.
又∵OM=BM=1,OP=OA=2,
∴OP=2OM,
∴∠MPO=30°,∠MOP=60°,
∴∠AOP=30°.
∴S扇形AOB=
=π,S扇形BMQ=
=
,S△MOP=
OM•OPsin60°=
×1×2×
=
,S扇形OAP=
=
,
∴S阴影=S扇形AOB-S扇形BMQ-S△MOP-S扇形OAP=
π-
.
故答案为:
π-
.
 解:如图,连结OP.
解:如图,连结OP.∵AO⊥OB,MP∥OA,
∴MP⊥OB.
又∵OM=BM=1,OP=OA=2,
∴OP=2OM,
∴∠MPO=30°,∠MOP=60°,
∴∠AOP=30°.
∴S扇形AOB=
| 90π×22 |
| 360 |
| 90π×12 |
| 360 |
| π |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| 30π×22 |
| 360 |
| π |
| 3 |
∴S阴影=S扇形AOB-S扇形BMQ-S△MOP-S扇形OAP=
| 5 |
| 12 |
| ||
| 2 |
故答案为:
| 5 |
| 12 |
| ||
| 2 |
点评:本题考查了扇形面积的计算.求阴影面积的主要思路是将不规则图形面积转化为规则图形的面积.

练习册系列答案
相关题目
 如图,AC∥EF∥BD.
如图,AC∥EF∥BD. 如图,圆的两弦的延长线交圆外于点P,若PC=4,CD=3,A为PB中点,求PB的长.
如图,圆的两弦的延长线交圆外于点P,若PC=4,CD=3,A为PB中点,求PB的长.