题目内容
16．
如图，在菱形ABCD中，点E是边AD的中点，EF⊥AC，交AB边于G，交CB的延长线于点F，求证：AB与EF互相平分．
分析 由菱形的性质可证AC⊥BD，又已知EF⊥AC，所以BD∥EF，可证四边形EDBF为平行四边形，可证AE=BF，即证结论．
解答 证明：连接BD，AF，BE，
在菱形ABCD中，AC⊥BD，
∵EF⊥AC，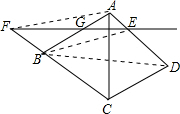
∴EF∥BD，
又∵ED∥FB，
∴四边形EDBF是平行四边形，DE=BF，
∵E为AD的中点，
∴AE=ED，
∴AE=BF，
又∵AE∥BF，
∴四边形AEBF为平行四边形，
∴AB与EF互相平分．
点评 本题是简单的推理证明题，主要考查菱形的性质，同时综合利用平行四边形的判定方法及中位线的性质，难度一般．
练习册系列答案
口算小状元口算速算天天练系列答案
相关题目
如图，△ABC三条角平分线AD、BE，CF交于点G，GH⊥BC于H，求证：∠BGD=∠CGH．
如图，在梯形ABCD中，AB∥CD，AB=15，CD=30，点E，F分别为AD，BC上一点，且EF∥AB．若梯形AEFB∽梯形EDCF，求线段EF的长．
用4个完全相同的立方体搭成如图所示的几何体，从左面看到的图形是（ ）
