题目内容
20.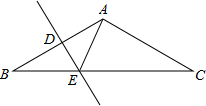 如图所示,底边BC为3$\sqrt{3}$,顶角A为120°的等腰△ABC中,DE垂直平分AB于D,则AE的长为( )
如图所示,底边BC为3$\sqrt{3}$,顶角A为120°的等腰△ABC中,DE垂直平分AB于D,则AE的长为( )| A. | 2$\sqrt{3}$ | B. | 2+$\sqrt{3}$ | C. | $\sqrt{3}$ | D. | 3$\sqrt{3}$ |
分析 ,根据等腰三角形的性质得到∠B=∠C=30°,根据线段垂直平分线的性质得到BE=AE,即可得到结论.
解答 解:∵AB=AC,∠A=120°,
∴∠B=∠C=30°,
∵DE垂直平分AB,
∴BE=AE,
∴∠B=∠BAE=30°,
∴∠EAC=90°,
∴AE=$\frac{1}{2}$CE,
∴AE+CE=3AE=BC,
∴AE=$\sqrt{3}$.
故选C.
点评 本题考查了线段垂直平分线性质,三角形的内角和定理,等腰三角形的性质,含30度角的直角三角形性质等知识点,主要考查运用性质进行推理的能力.

练习册系列答案
相关题目
10.下列图案不是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
10.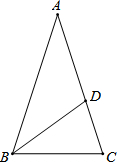 如图所示,已知在△ABC中,AB=AC,BC=BD,AD=DB,则∠A的度数是( )
如图所示,已知在△ABC中,AB=AC,BC=BD,AD=DB,则∠A的度数是( )
 如图所示,已知在△ABC中,AB=AC,BC=BD,AD=DB,则∠A的度数是( )
如图所示,已知在△ABC中,AB=AC,BC=BD,AD=DB,则∠A的度数是( )| A. | 30° | B. | 36° | C. | 45° | D. | 54° |
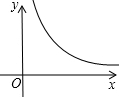 如图,在平面直角坐标系中,已知等边△OAB的顶点A在反比例函数y=$\frac{4\sqrt{3}}{x}$(x>0)图象上,当等边△OAB的顶点B在坐标轴上时,求等边△OAB顶点A的坐标和△OAB的面积.
如图,在平面直角坐标系中,已知等边△OAB的顶点A在反比例函数y=$\frac{4\sqrt{3}}{x}$(x>0)图象上,当等边△OAB的顶点B在坐标轴上时,求等边△OAB顶点A的坐标和△OAB的面积.