题目内容
5.计算:(1)-20+(-17)-(-18)-11;
(2)23-6×(-3)2+2×(-4);
(3)-1.53×0.75+0.53×$\frac{3}{4}$-3.4×0.75;
(4)54÷$\frac{3}{4}$-(-54)÷$\frac{1}{2}$+54÷(-$\frac{1}{4}$).
分析 (1)从左向右依次计算,求出算式的值是多少即可.
(2)首先计算乘方和乘法,然后从左向右依次计算,求出算式的值是多少即可.
(3)根据乘法分配律计算即可.
(4)首先计算除法,然后从左向右依次计算即可.
解答 解:(1)-20+(-17)-(-18)-11
=-37+18-11
=-19-11
=-30
(2)23-6×(-3)2+2×(-4)
=23-54-8
=-39
(3)-1.53×0.75+0.53×$\frac{3}{4}$-3.4×0.75
=-1.53×0.75+0.53×0.75-3.4×0.75
=(-1.53+0.53-3.4)×0.75
=-4.4×0.75
=-4×0.75×1.1
=-3×1.1
=-3.3
(4)54÷$\frac{3}{4}$-(-54)÷$\frac{1}{2}$+54÷(-$\frac{1}{4}$)
=72+108-216
=180-216
=-36
点评 此题主要考查了有理数的混合运算,要熟练掌握,注意明确有理数混合运算顺序:先算乘方,再算乘除,最后算加减;同级运算,应按从左到右的顺序进行计算;如果有括号,要先做括号内的运算,注意乘法分配律的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.幼儿园的阿姨给小朋友分苹果,如果每人3个还差3个,如果每人2个又多2个,则小朋友的人数为( )
| A. | 4个 | B. | 5个 | C. | 10个 | D. | 12个 |
13.下列各近似数精确到万位的是( )
| A. | 8200 | B. | 8亿5千万 | C. | 4×104 | D. | 12.5×104 |
20.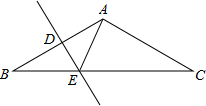 如图所示,底边BC为3$\sqrt{3}$,顶角A为120°的等腰△ABC中,DE垂直平分AB于D,则AE的长为( )
如图所示,底边BC为3$\sqrt{3}$,顶角A为120°的等腰△ABC中,DE垂直平分AB于D,则AE的长为( )
 如图所示,底边BC为3$\sqrt{3}$,顶角A为120°的等腰△ABC中,DE垂直平分AB于D,则AE的长为( )
如图所示,底边BC为3$\sqrt{3}$,顶角A为120°的等腰△ABC中,DE垂直平分AB于D,则AE的长为( )| A. | 2$\sqrt{3}$ | B. | 2+$\sqrt{3}$ | C. | $\sqrt{3}$ | D. | 3$\sqrt{3}$ |
14.若一个直角三角形的三边长分别为a、b、c,已知a2=25,b2=144,则c2=( )
| A. | 169 | B. | 119 | C. | 13或25 | D. | 169或119 |
15. 如图,直线y=-x+m与y=x+4的横坐标是-2,则关于不等式-x+m>x+4>0的整数解为( )
如图,直线y=-x+m与y=x+4的横坐标是-2,则关于不等式-x+m>x+4>0的整数解为( )
 如图,直线y=-x+m与y=x+4的横坐标是-2,则关于不等式-x+m>x+4>0的整数解为( )
如图,直线y=-x+m与y=x+4的横坐标是-2,则关于不等式-x+m>x+4>0的整数解为( )| A. | -1 | B. | -5 | C. | -4 | D. | -3 |