题目内容
12.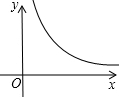 如图,在平面直角坐标系中,已知等边△OAB的顶点A在反比例函数y=$\frac{4\sqrt{3}}{x}$(x>0)图象上,当等边△OAB的顶点B在坐标轴上时,求等边△OAB顶点A的坐标和△OAB的面积.
如图,在平面直角坐标系中,已知等边△OAB的顶点A在反比例函数y=$\frac{4\sqrt{3}}{x}$(x>0)图象上,当等边△OAB的顶点B在坐标轴上时,求等边△OAB顶点A的坐标和△OAB的面积.
分析 根据等边三角形的性质和反比例系数k的几何意义即可求得A的在以及三角形AOC的面积,进而求得三角形AOB的面积.
解答  解:当点B在x轴上时,如图1,
解:当点B在x轴上时,如图1,
作AC⊥OB于C,
∵△AOB是等边三角形,
设OC=x,
∴AC=$\sqrt{3}$x,
∴A(x,$\sqrt{3}$x),
∵顶点A在反比例函数y=$\frac{4\sqrt{3}}{x}$(x>0)图象上,
∴x•$\sqrt{3}$x=4 $\sqrt{3}$,
∴x=2,
∴A(2,2 $\sqrt{3}$);
当点B在y轴上时,如图2,
作AC⊥y轴于C,
∵△AOB是等边三角形,
设OC=y,
∴AC=$\sqrt{3}$y,
∴A($\sqrt{3}$y,y),
∵顶点A在反比例函数y=$\frac{4\sqrt{3}}{x}$(x>0)图象上,
∴$\sqrt{3}$y•y=4$\sqrt{3}$,
∴y=2,
∴A(2$\sqrt{3}$,2);
S△AOB=2×$\frac{1}{2}$×4$\sqrt{3}$=4$\sqrt{3}$.
点评 本题考查了等边三角形的性质,反比例函数系数k的几何意义,反比例函数图象上点的坐标特征,关键是分类思想的运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.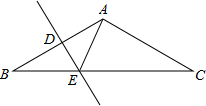 如图所示,底边BC为3$\sqrt{3}$,顶角A为120°的等腰△ABC中,DE垂直平分AB于D,则AE的长为( )
如图所示,底边BC为3$\sqrt{3}$,顶角A为120°的等腰△ABC中,DE垂直平分AB于D,则AE的长为( )
 如图所示,底边BC为3$\sqrt{3}$,顶角A为120°的等腰△ABC中,DE垂直平分AB于D,则AE的长为( )
如图所示,底边BC为3$\sqrt{3}$,顶角A为120°的等腰△ABC中,DE垂直平分AB于D,则AE的长为( )| A. | 2$\sqrt{3}$ | B. | 2+$\sqrt{3}$ | C. | $\sqrt{3}$ | D. | 3$\sqrt{3}$ |
1.已知反比例函数y=$\frac{2}{x}$,则在这个反比例函数图象上的点是( )
| A. | (-2,1) | B. | (1,2) | C. | (1,-2) | D. | (-2,-2) |
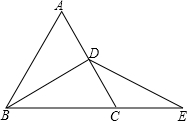 如图,△ABC为等边三角形,BD⊥AC于D,点E在BC的延长线上,且CE=CD,求证:BD=DE.
如图,△ABC为等边三角形,BD⊥AC于D,点E在BC的延长线上,且CE=CD,求证:BD=DE. 画出从正面、上面看到的几何体的形状图.
画出从正面、上面看到的几何体的形状图.