题目内容
14.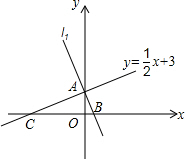 如图,直线y=$\frac{1}{2}$x+3与y轴交于点A、与x轴交于点C,直线l1与y轴交于点A,与x轴交于点B,且两直线互相垂直.
如图,直线y=$\frac{1}{2}$x+3与y轴交于点A、与x轴交于点C,直线l1与y轴交于点A,与x轴交于点B,且两直线互相垂直.(1)点A的坐标为(0,3),点B的坐标为($\frac{3}{2}$,0),点C的坐标为(-6,0).
(2)已知双曲线y=-$\frac{k}{x}$与l1交点坐标为(-1,k),求k的值;
(3)请利用图象直接写出不等式-$\frac{k}{x}$>$\frac{1}{2}$x+3的解集.
分析 (1)由y=$\frac{1}{2}$x+3得,x=0时,y=3,y=0时,x=-6,于是得到A(0,3),C(-6,0),求出直线l1的解析式为:y=-2x+3;当y=0时,x=$\frac{3}{2}$,于是得到B($\frac{3}{2}$,0);
(2)把x=-1代入y=-2x+3即可得到结论;
(3)根据两个图象的交点坐标,即可得出答案.
解答 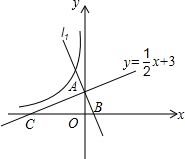 解:(1)由y=$\frac{1}{2}$x+3得,x=0时,y=3,y=0时,x=-6,
解:(1)由y=$\frac{1}{2}$x+3得,x=0时,y=3,y=0时,x=-6,
∴A(0,3),C(-6,0),
∵直线l1与直线y=$\frac{1}{2}$x+3垂直,
∴设直线l1的解析式为:y=-2x+b,
∵直线l1与y轴交于点A,
∴b=3,
∴直线l1的解析式为:y=-2x+3;
当y=0时,x=$\frac{3}{2}$,
∴B($\frac{3}{2}$,0);
故答案为:(0,3),($\frac{3}{2}$,0),(-6,0),
(2)把x=-1代入y=-2x+3得y=-5,
∴k=-5;
(3)由图象可知不等式-$\frac{k}{x}$>$\frac{1}{2}$x+3的解集为x<0.
点评 本题考查了反比例函数与一次函数的交点,待定系数法求反比例函数的解析式,掌握待定系数法求函数解析式的一般步骤是解题的关键,注意数形结合思想的运用.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
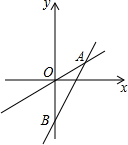 正比例函数y=k1x与一次函数y=k2x+b的图象如图所示,它们的交点A的坐标为(3,4),且OB=10.
正比例函数y=k1x与一次函数y=k2x+b的图象如图所示,它们的交点A的坐标为(3,4),且OB=10.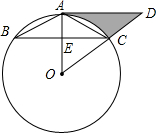 如图,⊙O为△ABC的外接圆,AB=AC,AD∥BC交OC的延长线于点D.
如图,⊙O为△ABC的外接圆,AB=AC,AD∥BC交OC的延长线于点D.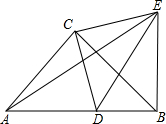 如图,△ACB和△DCE都是等腰直角三角形,∠ACB=∠DCE=90°,D为AB边上-点.
如图,△ACB和△DCE都是等腰直角三角形,∠ACB=∠DCE=90°,D为AB边上-点.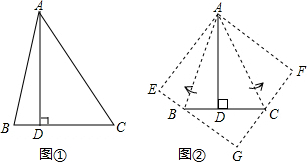
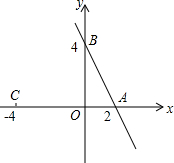 如图,直线y=-2x+b与x轴,y轴分别相交于A、B两点,点B的坐标为(0,4),点C的坐标为(-4,0).
如图,直线y=-2x+b与x轴,y轴分别相交于A、B两点,点B的坐标为(0,4),点C的坐标为(-4,0).