题目内容
5.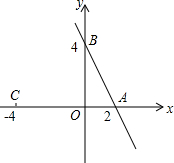 如图,直线y=-2x+b与x轴,y轴分别相交于A、B两点,点B的坐标为(0,4),点C的坐标为(-4,0).
如图,直线y=-2x+b与x轴,y轴分别相交于A、B两点,点B的坐标为(0,4),点C的坐标为(-4,0).(1)直线AB的解析式为y=-2x+4.
(2)点A的坐标为(2,0),AC的长为6.
(3)若动点P(x,y)在直线AB上,则△PAC中AC边上的高=|-2x+4|(用含x的式子表示),其中x的取值范围为x≠2.
(4)若△PAC的面积为6,试确定点P的坐标.
分析 (1)将点B的坐标代入带直线解析式中可求出b值,从而得出结论;
(2)令y=0,求出此时x的值即可得出点A的坐标,结合A、C点的坐标即可得出线段AC的长度;
(3)由AC在x轴,结合坐标系中点的意义可得出△PAC中AC边上的高为|y|,结合点P在直线AB上即可得出结论;
(4)由线段AC的长度结合三角形的面积公式即可求出P点的纵坐标,再依据点P在直线AB上,即可得出点P的坐标.
解答 解:(1)∵点B在直线y=-2x+b的图象上,
∴4=-2×0+b,b=4,
∴直线AB的解析式为y=-2x+4.
故答案为:y=-2x+4.
(2)令y=-2x+4中的y=0,
则有0=-2x+4,解得:x=2.
∴点A的坐标为(2,0),AC=2-(-4)=6.
故答案为:(2,0);6.
(3)∵AC边在x轴上,且点P的坐标为(x,y),
∴△PAC中AC边上的高=|y|=|-2x+4|.
∵y≠0,即-2x+4≠0,
解得:x≠2.
故答案为:|-2x+4|;x≠2.
(4)∵AC=6,
∴S△PAC=$\frac{1}{2}$AC•|y|=6,
解得:y=±2,
当y=2时,有-2x+4=2,解得:x=1;
当y=-2时,有-2x+4=-2,解得:x=3.
故点P的坐标为(1,2)或(3,-2).
点评 本题考查了一次函数的性质、待定系数法求函数解析式以及三角形的面积公式,解题的关键是:(1)求出b值;(2)求出点A的坐标;(3)由点在直线上,得出点坐标的特点;(4)结合三角形的面积公式计算出P点的纵坐标.本题属于基础题,难度不大,解决该题型题目时,结合一次函数的性质解决问题是关键.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
17.若实数a、b满足a+b=0,且a<b,则一次函数y=ax+b的图象不可能经过( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
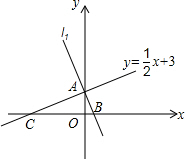 如图,直线y=$\frac{1}{2}$x+3与y轴交于点A、与x轴交于点C,直线l1与y轴交于点A,与x轴交于点B,且两直线互相垂直.
如图,直线y=$\frac{1}{2}$x+3与y轴交于点A、与x轴交于点C,直线l1与y轴交于点A,与x轴交于点B,且两直线互相垂直.
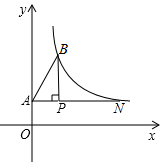 如图,点P的坐标为(2,$\frac{3}{2}$),过点P作x轴的平行线交y轴于点A,作PB⊥AP交反比例函数y=$\frac{k}{x}$(x>0)于点B,连结AB.已知tan∠BAP=$\frac{3}{2}$.
如图,点P的坐标为(2,$\frac{3}{2}$),过点P作x轴的平行线交y轴于点A,作PB⊥AP交反比例函数y=$\frac{k}{x}$(x>0)于点B,连结AB.已知tan∠BAP=$\frac{3}{2}$.