题目内容
9.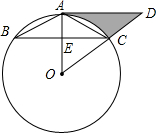 如图,⊙O为△ABC的外接圆,AB=AC,AD∥BC交OC的延长线于点D.
如图,⊙O为△ABC的外接圆,AB=AC,AD∥BC交OC的延长线于点D.(1)求证:AD为⊙O的切线;
(2)若AB∥DC,AD=3,求阴影部分的面积.
分析 (1)欲证明AD为⊙O的切线,只要证明∠DAO=90°,根据垂径定理可以证明OA⊥BC,因为AD∥BC,所以不难证明∠DAO=90°.
(2)先证明△AOC是等边三角形,根据阴影部分的面积=S△ADO-S扇形AOC进行计算即可.
解答 (1)证明:∵AB=AC,
∴$\widehat{AB}$=$\widehat{AC}$,
∴OA⊥BC,
∴∠OEC=90°,
∵AD∥BC,
∴∠OAD=∠OEC=90°,
∴OA⊥AD,
∴AD是⊙O的切线.
(2)解:∵AB∥DC,
∴∠ABC=∠BCO,
∵AB=AC,
∴∠ACE=∠ABC=∠OCE,
∵∠CAE+∠ACE=90°,∠COA+∠OCE=90°,
∴∠CAO=∠COA,
∴CA=OC=AO,
∴△AOC是等边三角形,
∴AO=OC=AD=2,∠AOC=60°,
在RT△AOD中,∵OA=2,∠D=30°,
∴AD=$\sqrt{3}$AO=2$\sqrt{3}$
∴阴影部分的面积=S△ADO-S扇形AOC=$\frac{1}{2}$•AD•OA-$\frac{60π•{2}^{2}}{360}$=2$\sqrt{3}$-$\frac{2π}{3}$.
点评 本题考查切线的判定、等边三角形的判定和性质、扇形的面积等知识,解题的关键是熟练掌握切线的判定方法,学会利用分割法求面积,所以中考常考题型.

练习册系列答案
相关题目
20.某市为了加快城市建设力度.2014年市政府共投资2亿元人民币,预计到2016年底三年共累计投资9.5亿元人民币,若在这两年内每年投资的增长率都为x,可列方程( )
| A. | 2x2=9.5 | B. | 2+2(x+1)+2(x+1)2=9.5 | ||
| C. | 2(x+1)2=9.5 | D. | 2+(x+1)+(x+1)2=9 |
17.下列分式方程有解的是( )
| A. | $\frac{1}{2x-3}$=0 | B. | $\frac{{x}^{2}+1}{x}$=0 | C. | $\frac{2x}{x-1}=\frac{x+1}{x-1}$ | D. | $\frac{1}{x-1}=1$ |
 如图,AB、CD相交于点O,EO⊥DC,∠AOE的余角是∠AOD,∠COB的补角是∠AOC和∠BOD.
如图,AB、CD相交于点O,EO⊥DC,∠AOE的余角是∠AOD,∠COB的补角是∠AOC和∠BOD.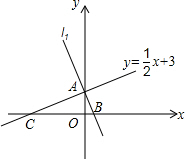 如图,直线y=$\frac{1}{2}$x+3与y轴交于点A、与x轴交于点C,直线l1与y轴交于点A,与x轴交于点B,且两直线互相垂直.
如图,直线y=$\frac{1}{2}$x+3与y轴交于点A、与x轴交于点C,直线l1与y轴交于点A,与x轴交于点B,且两直线互相垂直.
 如图,已知AD∥BC,∠1=∠2,说明BE∥DF的理由.
如图,已知AD∥BC,∠1=∠2,说明BE∥DF的理由.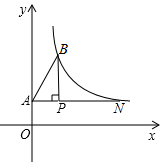 如图,点P的坐标为(2,$\frac{3}{2}$),过点P作x轴的平行线交y轴于点A,作PB⊥AP交反比例函数y=$\frac{k}{x}$(x>0)于点B,连结AB.已知tan∠BAP=$\frac{3}{2}$.
如图,点P的坐标为(2,$\frac{3}{2}$),过点P作x轴的平行线交y轴于点A,作PB⊥AP交反比例函数y=$\frac{k}{x}$(x>0)于点B,连结AB.已知tan∠BAP=$\frac{3}{2}$.