Question

1．已知：如图，在△ABC中，∠ABC的平分线BP与AC边的垂直平分线PQ交于点P，过点P分别作PD⊥AB于点D，PE⊥BC于点E，若BE=10cm，AB=6cm，求CE的长．

Answer 1

分析 先证△BPD≌△BPE得BD=BE，根据BE=10cm、AB=6cm可得AD的长，再证RT△PAD≌RT△PCE得CE=AD即可．

解答 解：如图，连接AP、CP，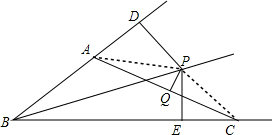

∵BP平分∠ABC，PD⊥AB，PE⊥BC，
∴∠PBD=∠PBE，∠PDB=∠PEC=90°，PD=PE，
在△BPD和△BPE中，
$\left\{\begin{array}{l}{∠PBD=∠PBE}\\{∠PDB=∠PEC}\\{BP=BP}\end{array}\right.$，
∴△BPD≌△BPE（AAS），
∴BD=BE，
又∵BE=10cm，AB=6cm，
∴AD=BD-AB=BE-AB=4cm，
∵PQ垂直平分AC，
∴PA=PC，
在RT△PAD和RT△PCE中，
$\left\{\begin{array}{l}{PD=PE}\\{PA=PC}\end{array}\right.$，
∴RT△PAD≌RT△PCE（HL），
∴CE=AD=4cm．

点评 本题主要考查全等三角形的判定与性质，能根据题目的需要构建有用的全等三角形是关键