题目内容
1.当x,y分别取何值时,多项式x2+y2-2x+2y+10的值最小?最小值为多少?分析 原式配方后,利用非负数的性质求出最小值即可.
解答 解:∵原式=(x-1)2+(y+1)2+8≥8,
∴当x=1,y=-1时,多项式x2+y2-2x+2y+10的值最小,最小值为8.
点评 此题考查了配方法的应用,以及非负数的性质:偶次方,熟练掌握完全平方公式是解本题的关键.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
9.下列说法中错误的是( )
| A. | π的值等于3.14 | B. | π的值是圆周长与直径的比值 | ||
| C. | π的值与圆的大小无关 | D. | π是一个无限小数 |
11.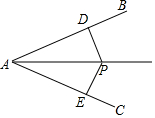 如图,点P在∠BAC的角平分线上,PD⊥AB,PE⊥AC,垂足分别为D、E,则△APD与△APE全等的理由是( )
如图,点P在∠BAC的角平分线上,PD⊥AB,PE⊥AC,垂足分别为D、E,则△APD与△APE全等的理由是( )
 如图,点P在∠BAC的角平分线上,PD⊥AB,PE⊥AC,垂足分别为D、E,则△APD与△APE全等的理由是( )
如图,点P在∠BAC的角平分线上,PD⊥AB,PE⊥AC,垂足分别为D、E,则△APD与△APE全等的理由是( )| A. | SAS | B. | AAS | C. | SSS | D. | HL |
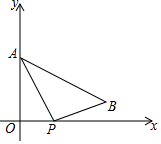 如图,在平面直角坐标系中,点A(0,3)、点B(4,1),点P是x轴正半轴上一动点.给出4个结论:
如图,在平面直角坐标系中,点A(0,3)、点B(4,1),点P是x轴正半轴上一动点.给出4个结论: 已知,正六边形ABCDEF在直角坐标系内的位置如图所示,点A的坐标为A(-1,0),点B在原点,把正六边形ABCDEF沿x轴正半轴作无滑动的连续翻转,每次翻转60°,经过2016次翻转之后,点B的经过的路径长是(2016$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$).
已知,正六边形ABCDEF在直角坐标系内的位置如图所示,点A的坐标为A(-1,0),点B在原点,把正六边形ABCDEF沿x轴正半轴作无滑动的连续翻转,每次翻转60°,经过2016次翻转之后,点B的经过的路径长是(2016$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$).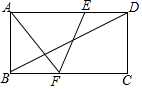 如图,在矩形ABCD中,点E、F分别是AD、BC上的点,连接AF、EF,EF与对角线BD交于点O.若AE=AF=CF=12,∠AEF=2∠ADB,则矩形ABCD的面积为108$\sqrt{3}$.
如图,在矩形ABCD中,点E、F分别是AD、BC上的点,连接AF、EF,EF与对角线BD交于点O.若AE=AF=CF=12,∠AEF=2∠ADB,则矩形ABCD的面积为108$\sqrt{3}$.