题目内容
6.在△ABC中,BC=2$\sqrt{3}$,AB=c,AB边上的中线CD=m,且c,m满足c2+m2-8c-4m+20=0,则∠A的度数是30°.分析 由配方法可求出c与m的值,从而可知△ABC是直角三角形,利用锐角三角函数即可求出答案.
解答 解:∵c2+m2-8c-4m+20=0,
∴c2-8c+16+m2-4m+4=0
∴(c-4)2+(m-2)2=0,
∴c=4,m=2,
∴AB=4,CD=2,
∴AB=2CD,
∵CD是AB边上的中线,
∴∠ACB=90°,
∴在Rt△ABC中,
∴sin∠A=$\frac{BC}{AB}$=$\frac{\sqrt{3}}{2}$,
∴∠A=30°
故答案为:30°
点评 本题考查配方法的应用,涉及配方法的应用,非负数的性质,含30度的直角三角形,本题属于中等题型.

练习册系列答案
相关题目
14.刘亮的妈妈每天早上要送新鲜蔬菜到市场去卖,下面是她一周送出的20筐菜的重量记录表,每筐以25kg为标准重量.
求她一周送出20筐新鲜蔬菜的总质量.
| 筐数 | 2 | 5 | 3 | 4 | 2 | 4 |
| 与标准质量相比(kg) | -0.8 | +0.6 | -0.5 | +0.4 | +0.5 | -0.3 |
 如图,正方形ABCD的面积为1.△BPC为等边三角形.则△PBD的面积为$\frac{\sqrt{3}-1}{4}$.
如图,正方形ABCD的面积为1.△BPC为等边三角形.则△PBD的面积为$\frac{\sqrt{3}-1}{4}$.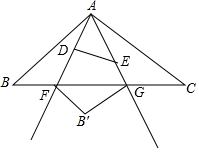 如图,在△ABC中,AB=AC=4,∠BAC=90°,以A为一个顶点的等腰Rt△ADE,∠ADE=90°,绕点A在∠BAC内旋转,AD、AE所在的直线与BC边分别交于点F、G,若点B关于直线AD的对称点为B′,当∠CFB′=60°时,则BF的长为$\frac{6\sqrt{2}-2\sqrt{3}}{3}$.
如图,在△ABC中,AB=AC=4,∠BAC=90°,以A为一个顶点的等腰Rt△ADE,∠ADE=90°,绕点A在∠BAC内旋转,AD、AE所在的直线与BC边分别交于点F、G,若点B关于直线AD的对称点为B′,当∠CFB′=60°时,则BF的长为$\frac{6\sqrt{2}-2\sqrt{3}}{3}$.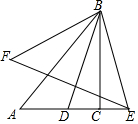 如图,在Rt△BAC中,∠ACB=Rt∠,AC=6,BC=8,D是AC边上的一点,点D关于BC的对称点为E,关于AB的对称点为F,连接BD,BE,BF,EF,若BD平分∠ABC,则EF的长为$\frac{16}{5}\sqrt{10}$.
如图,在Rt△BAC中,∠ACB=Rt∠,AC=6,BC=8,D是AC边上的一点,点D关于BC的对称点为E,关于AB的对称点为F,连接BD,BE,BF,EF,若BD平分∠ABC,则EF的长为$\frac{16}{5}\sqrt{10}$.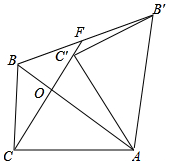 如图,在Rt△ABC中,∠ACB=90°,tan∠CBA=$\frac{4}{3}$,AB=5.将△ABC绕点A顺时针旋转得到△AB′C′,连接CC′并延长,交AB于点O,交BB′于点F.若CC′=CA,则BF=$\frac{5}{2}$.
如图,在Rt△ABC中,∠ACB=90°,tan∠CBA=$\frac{4}{3}$,AB=5.将△ABC绕点A顺时针旋转得到△AB′C′,连接CC′并延长,交AB于点O,交BB′于点F.若CC′=CA,则BF=$\frac{5}{2}$.