题目内容
18. 如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作正△ABC和正△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ.以下五个结论:
如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作正△ABC和正△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ.以下五个结论:①AD=BE;②PQ∥AE;③AP=BQ;④CO平分∠AOE;⑤∠AOB=60°.
恒成立的结论有①②③④⑤.(把你认为正确的序号都填上)
分析 证明①可先证明△ACD≌△BCE,已有:AB=BC,CD=CE,易得∠ACD=∠BCE,其他的证明需要通过①得到,再利用三角形相似以及等边三角形的知识分别进行证明即可得出答案.
解答 解:①∵△ABC和△CDE为等边三角形
∴AC=BC,CD=CE,∠BCA=∠DCB=60°
∴∠ACD=∠BCE
在△ACD和△BCE中,
$\left\{\begin{array}{l}{AC=CB}\\{∠ACD=∠BCE}\\{CD=CE}\end{array}\right.$,
∴△ACD≌△BCE
∴AD=BE,故①正确;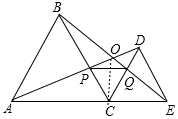
由(1)中的全等得∠CBE=∠DAC,进而可求证△CQB≌△CPA,
∴AP=BQ,故③正确;
又∵∠PCQ=60°可知△PCQ为等边三角形,
∴∠PQC=∠DCE=60°,
∴PQ∥AE②成立,
∵BC∥DE,
∴∠CBE=∠BED,
∵∠CBE=∠DAE,
∴∠AOB=∠OAE+∠AEO=60°,故⑤正确;
∴∠AOE=120°,
∵∠PBO=∠PAC,∠BOP=∠PCA,
∴△BPO∽△APC,
∴$\frac{PB}{AP}$=$\frac{OP}{PC}$,
∴$\frac{PB}{OP}$=$\frac{AP}{PC}$,∵∠APB=∠CPO,
∴△APB∽△CPO,
∴∠COP=∠ABP=60°,
∴∠COA=∠COB=60°,故④正确,
故正确的有①②③④⑤,
故答案为①②③④⑤.
点评 此题主要考查了等边三角形的性质、全等三角形的判定与性质、相似三角形的判定与性质,熟练应用三角形全等的证明以及相似三角形的判定是正确解答本题的关键.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
8.拒绝“餐桌浪费”,刻不容缓.据统计全国每年浪费食物总量约50 000 000 000kg,这个数据用科学记数法表示为( )
| A. | 0.5×1011kg | B. | 50×109kg | C. | 5×109kg | D. | 5×1010kg |
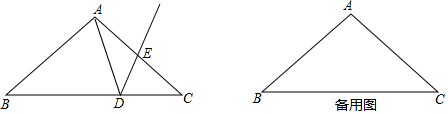
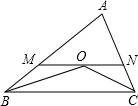 如图,△ABC中,∠ABC、∠ACB的平分线相交于O,MN过点O且与BC平行.△ABC的周长为20,△AMN的周长为12,则BC的长为( )
如图,△ABC中,∠ABC、∠ACB的平分线相交于O,MN过点O且与BC平行.△ABC的周长为20,△AMN的周长为12,则BC的长为( )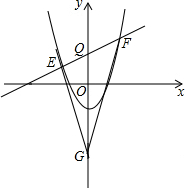 如图,抛物线y=$\frac{1}{2}$x2-2交y轴于C,不平行于x轴的直线y=kx+3交抛物线于E、F,交y轴于点Q,在y轴的负半轴上是否存在点G使EQ•FG=FQ•EG,若存在,请求出G点坐标;若不存在.请说明理由.
如图,抛物线y=$\frac{1}{2}$x2-2交y轴于C,不平行于x轴的直线y=kx+3交抛物线于E、F,交y轴于点Q,在y轴的负半轴上是否存在点G使EQ•FG=FQ•EG,若存在,请求出G点坐标;若不存在.请说明理由.