题目内容
11.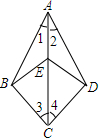 已知:如图,∠1=∠2,∠3=∠4.求证:∠AEB=∠AED.
已知:如图,∠1=∠2,∠3=∠4.求证:∠AEB=∠AED.
分析 利用ASA得到三角形ABC与三角形ADC全等,利用全等三角形的性质得到AB=AD,再利用SAS得到三角形ABE与三角形ADE全等,利用全等三角形对应角相等即可得证.
解答 证明:在△ABC和△ADC中,
$\left\{\begin{array}{l}{∠1=∠2}\\{AC=AC}\\{∠3=∠4}\end{array}\right.$,
∴△ABC≌△ADC(ASA),
∴AB=AD,
在△ABE和△ADE中,
$\left\{\begin{array}{l}{AB=AD}\\{∠1=∠2}\\{AE=AE}\end{array}\right.$,
∴△ABE≌△ADE(SAS),
∴∠AEB=∠AED.
点评 此题考查了全等三角形的判定与性质,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
相关题目
1.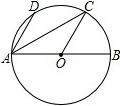 如图,AB是⊙O的直径,AB=4,D、C在⊙O上,AD∥OC,∠DAB=60°,连接AC,则AC=( )
如图,AB是⊙O的直径,AB=4,D、C在⊙O上,AD∥OC,∠DAB=60°,连接AC,则AC=( )
 如图,AB是⊙O的直径,AB=4,D、C在⊙O上,AD∥OC,∠DAB=60°,连接AC,则AC=( )
如图,AB是⊙O的直径,AB=4,D、C在⊙O上,AD∥OC,∠DAB=60°,连接AC,则AC=( )| A. | 4 | B. | $\sqrt{3}$ | C. | $2\sqrt{3}$ | D. | $\sqrt{6}$ |
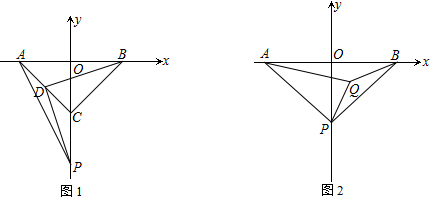
 如图,矩形PABC的顶点P在抛物线y=-(x-1)2-2上运动,点A、B均在x轴上,且PC=2PA,则矩形PABC周长的最小值为12.
如图,矩形PABC的顶点P在抛物线y=-(x-1)2-2上运动,点A、B均在x轴上,且PC=2PA,则矩形PABC周长的最小值为12.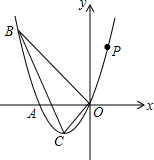 如图,已知抛物线经过点A(-2,0),点B(-3,3)及原点O,顶点为C.
如图,已知抛物线经过点A(-2,0),点B(-3,3)及原点O,顶点为C.