题目内容
10．
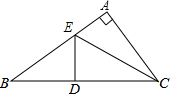如图，在△ABC中，∠A=90°，DE垂直平分BC，求证：BE2-AE2=AC2．
分析 根据垂直平分线的性质得出BE=EC，再利用勾股定理得出答案．
解答 证明：∵DE垂直平分BC，
∴BE=EC，
∵∠A=90°，
∴AE2+AC2=EC2，
∴AE2+AC2=EB2，
∴BE2-AE2=AC2．
点评 此题主要考查了勾股定理以及线段垂直平分线的性质，得出BE=EC是解题关键．
练习册系列答案
互动英语系列答案
相关题目
1．在平面直角坐标系中，已知A（1，0），B（2015，0），点P是该平面直角坐标系内的一个动点，则使∠APB=30°的点P有（ ）
| A． | 0个 | B． | 2014个 | C． | 2015个 | D． | 无数个 |
如图，在△ABC中，AB=AC=2，∠A=90°，点P为BC的中点，点E、F分别为边AB、AC上的点，若∠EPF=45°，∠FEP=60°，则CF=3-$\sqrt{3}$．
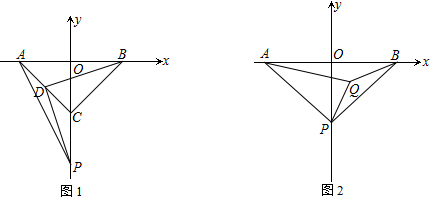
如图，矩形PABC的顶点P在抛物线y=-（x-1）2-2上运动，点A、B均在x轴上，且PC=2PA，则矩形PABC周长的最小值为12．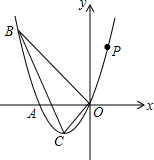
如图，已知抛物线经过点A（-2，0），点B（-3，3）及原点O，顶点为C．