题目内容
12.在△ABC中,∠C=90°,a=9,c=15,解这个直角三角形.分析 可根据勾股定理求出b的值,再根据三角函数的定义求出sinA,由此可得到∠A及∠A的余角∠B的值.
解答 解:∵∠C=90°,a=9,c=15,
∴根据勾股定理可得,
b=$\sqrt{{c}^{2}-{a}^{2}}$=$\sqrt{1{5}^{2}-{9}^{2}}$=12.
根据三角函数的定义可得,
sinA=$\frac{a}{c}$=$\frac{9}{15}$=$\frac{3}{5}$,
∴∠A≈37°,
∴∠B≈53°.
点评 本题主要考查了勾股定理、三角函数的定义,已知三角函数值求角度、余角等知识,在直角三角形中,除直角外,一共有五个元素,即三条边和两个锐角,由直角三角形中除直角外的已知元素求出所有未知元素的过程叫做解直角三角形解直角三角形.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
1.在平面直角坐标系中,已知A(1,0),B(2015,0),点P是该平面直角坐标系内的一个动点,则使∠APB=30°的点P有( )
| A. | 0个 | B. | 2014个 | C. | 2015个 | D. | 无数个 |
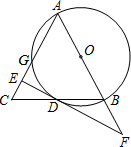 如图,以△ABC的边AB为直径的⊙O与BC、AC分别交于D,G,过D的切线垂直AC于E,与AB的延长线交于F.
如图,以△ABC的边AB为直径的⊙O与BC、AC分别交于D,G,过D的切线垂直AC于E,与AB的延长线交于F. 如图,矩形PABC的顶点P在抛物线y=-(x-1)2-2上运动,点A、B均在x轴上,且PC=2PA,则矩形PABC周长的最小值为12.
如图,矩形PABC的顶点P在抛物线y=-(x-1)2-2上运动,点A、B均在x轴上,且PC=2PA,则矩形PABC周长的最小值为12.