题目内容
4.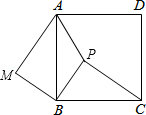 正方形ABCD内有一点P,连接AP,BP,CP,将△PBC绕点B逆时针旋转至BC与AB重合,得到△ABM.
正方形ABCD内有一点P,连接AP,BP,CP,将△PBC绕点B逆时针旋转至BC与AB重合,得到△ABM.(1)求证:PB⊥BM;
(2)若AP:PB=1:2,∠APB=135°,AM=3,求PM的长.
分析 (1)先由正方形的性质得出∠ABC=90°,再利用旋转的性质得到∠MBP=∠ABC=90°,即PB⊥BM;
(2)连结PM.设AP=k,则PB=2k.先证明△MBP为等腰直角三角形,那么PM=$\sqrt{2}$BP=2$\sqrt{2}$k,再求出∠APM=∠APB-∠BPM=90°,根据勾股定理得出AP2+PM2=AM2,即k2+(2$\sqrt{2}$k)2=32,解方程求出k=1,于是PM=2$\sqrt{2}$.
解答 (1)证明:∵四边形ABCD是正方形,
∴∠ABC=90°,
∵将△PBC绕点B逆时针旋转至BC与AB重合,得到△ABM,
∴△PBC≌△MBA,∠MBP=∠ABC=90°,
∴PB⊥BM;  (2)解:如图,连结PM.
(2)解:如图,连结PM.
设AP=k,则PB=2k.
由旋转的性质可得,BP=BM=2k,∠MBP=90°,
∴△MBP为等腰直角三角形,PM=$\sqrt{2}$BP=2$\sqrt{2}$k,
∴∠BPM=45°,
∵∠APB=135°,
∴∠APM=∠APB-∠BPM=90°,
∴AP2+PM2=AM2,即k2+(2$\sqrt{2}$k)2=32,
解得k=1(负值舍去),
∴PM=2$\sqrt{2}$.
点评 此题考查了旋转的性质,正方形的性质,勾股定理,等腰直角三角形的判定与性质等知识,根据旋转得出对应线段之间的等量关系,是解决问题的关键.

练习册系列答案
相关题目
13.当a=5时,下列代数式中值最大的是( )
| A. | 2a+3 | B. | $\frac{a}{2}$-1 | C. | $\frac{1}{5}$a2-2a+10 | D. | $\frac{7{a}^{2}-100}{5}$ |
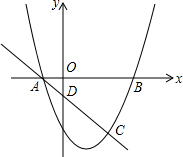 抛物线y=ax2+bx+c与x轴的交点为A(-1,0)和B(3,0),与直线y=-x+k相交于点A和点C(2,-3).
抛物线y=ax2+bx+c与x轴的交点为A(-1,0)和B(3,0),与直线y=-x+k相交于点A和点C(2,-3).