题目内容
12．将下列多项式因式分解，结果中不含有因式（x-2）的是（ ）| A． | x2-4 | B． | x3-4x2-12x | C． | x2-2x | D． | （x-3）2+2（x-3）+1 |
分析 对各多项式进行因式分解即可求出答案．
解答 解：（A）原式=（x+2）（x-2），结果中含有因式（x-2）；
（B）原式=x（x2-4x-12）=x（x+2）（x-6），结果中不含有因式（x-2）；
（C）原式=x（x-2），结果中含有因式（x-2）；
（D）原式=[（x-3）+1]2=（x-2）2，结果中含有因式（x-2）；
故选（B）
点评 本题考查因式分解，解题的关键是熟练运用因式分解的方法，本题属于基础题型．
练习册系列答案
阅读快车系列答案
相关题目
3．已知正方体的体积为2$\sqrt{2}$，则这个正方体的棱长为（ ）
| A． | 1 | B． | $\sqrt{2}$ | C． | $\sqrt{6}$ | D． | 3 |
20．
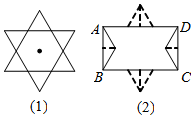小东同学对图形世界充满兴趣，他先把一个面积为$\frac{27}{4}\sqrt{3}$cm2的正三角形绕着它的中心旋转60°，旋转前后的两个正三角形构成如图（1）的一个六角星；然后将该六角星按图（2）分割后拼成矩形ABCD．请你思考小东的问
题：若将该矩形围成圆柱，则圆柱的高为（ ）
小东同学对图形世界充满兴趣，他先把一个面积为$\frac{27}{4}\sqrt{3}$cm2的正三角形绕着它的中心旋转60°，旋转前后的两个正三角形构成如图（1）的一个六角星；然后将该六角星按图（2）分割后拼成矩形ABCD．请你思考小东的问题：若将该矩形围成圆柱，则圆柱的高为（ ）
| A． | 2$\sqrt{3}$cm | B． | 3$\sqrt{3}$cm | C． | 2$\sqrt{3}$cm 或6 cm | D． | 3cm或3$\sqrt{3}$cm |
7．估计$\sqrt{48}$-$\frac{\sqrt{27}}{3}$的运算结果在（ ）
| A． | 3和4之间 | B． | 4和5之间 | C． | 5和6之间 | D． | 6和7之间 |
17．在实数-2，$\sqrt{2}$，0，-1中，最小的数是（ ）
| A． | -2 | B． | $\sqrt{2}$ | C． | 0 | D． | -1 |
小明对九（1）班同学“你最喜欢的球类项目是什么？（只选一项）”的问题进行了调查，把所得数据绘制成如图所示的扇形统计图．由图可知，该班同学最喜欢的球类项目是（ ）