题目内容
20. 小东同学对图形世界充满兴趣,他先把一个面积为$\frac{27}{4}\sqrt{3}$cm2的正三角形绕着它的中心旋转60°,旋转前后的两个正三角形构成如图(1)的一个六角星;然后将该六角星按图(2)分割后拼成矩形ABCD.请你思考小东的问
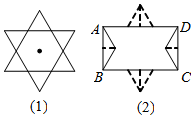
小东同学对图形世界充满兴趣,他先把一个面积为$\frac{27}{4}\sqrt{3}$cm2的正三角形绕着它的中心旋转60°,旋转前后的两个正三角形构成如图(1)的一个六角星;然后将该六角星按图(2)分割后拼成矩形ABCD.请你思考小东的问题:若将该矩形围成圆柱,则圆柱的高为( )
| A. | 2$\sqrt{3}$cm | B. | 3$\sqrt{3}$cm | C. | 2$\sqrt{3}$cm 或6 cm | D. | 3cm或3$\sqrt{3}$cm |
分析 先利用等边三角形的性质得到等边三角形的边长为3$\sqrt{3}$,从而得到AD=3$\sqrt{3}$,如图2,OH⊥AD于H,AH=$\frac{3\sqrt{3}}{2}$,利用含30度的直角三角形三边的关系得到OH=$\frac{\sqrt{3}}{3}$AH=$\frac{3}{2}$,所以AB=3,然后讨论:当母线为AD时,高为3$\sqrt{3}$cm;当母线为AB时,高为3cm.
解答 解:设正三角形的边长为x,则$\frac{\sqrt{3}}{4}$x2=$\frac{27\sqrt{3}}{4}$,解得x=3$\sqrt{3}$,
所以AD=3$\sqrt{3}$,
如图2,OH⊥AD于H,AH=$\frac{3\sqrt{3}}{2}$,
∴OH=$\frac{\sqrt{3}}{3}$AH=$\frac{\sqrt{3}}{3}$×$\frac{3\sqrt{3}}{2}$=$\frac{3}{2}$,
∴AB=2OH=3,
∴把矩形ABCD围成圆柱,则圆柱的高为3$\sqrt{3}$cm或3cm.
故选D.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查等边三角形的性质.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
10.下列图案中,既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
11.在下列图形中,既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
8. 如图,将一块直角三角板的直角顶点放在直尺的一边上.若∠2=40°,则∠1的度数是( )
如图,将一块直角三角板的直角顶点放在直尺的一边上.若∠2=40°,则∠1的度数是( )
 如图,将一块直角三角板的直角顶点放在直尺的一边上.若∠2=40°,则∠1的度数是( )
如图,将一块直角三角板的直角顶点放在直尺的一边上.若∠2=40°,则∠1的度数是( )| A. | 60° | B. | 50° | C. | 40° | D. | 30° |
15.如果a与2017互为倒数,那么a是( )
| A. | -2017 | B. | 2017 | C. | -$\frac{1}{2017}$ | D. | $\frac{1}{2017}$ |
5.在-2.5,$\frac{1}{3}$,0,2这四个数中,最小的数是( )
| A. | -2.5 | B. | $\frac{1}{3}$ | C. | 0 | D. | 2 |
12.将下列多项式因式分解,结果中不含有因式(x-2)的是( )
| A. | x2-4 | B. | x3-4x2-12x | C. | x2-2x | D. | (x-3)2+2(x-3)+1 |