题目内容
2.下列各组数,可以作为直角三角形的三边长的是( )| A. | 32,42,52 | B. | $\sqrt{2}$,$\sqrt{2}$,2 | C. | 2,3,4 | D. | $\sqrt{3}$,$\sqrt{4}$,$\sqrt{5}$ |
分析 分别求出两小边的平方和和长边的平方,看看是否相等即可.
解答 解:A、∵(32)2+(42)2≠(52)2,
∴以32、42、52为边不能组成直角三角形,故本选项不符合题意;
B、∵($\sqrt{2}$)2+($\sqrt{2}$)2=22,
∴以$\sqrt{2}$、$\sqrt{2}$、2为边能组成直角三角形,故本选项符合题意;
C、∵22+32≠42,
∴以2、3、4为边不能组成直角三角形,故本选项不符合题意;
D、∵($\sqrt{3}$)2+($\sqrt{4}$)2≠($\sqrt{5}$)2,
∴以$\sqrt{3}$、$\sqrt{4}$、$\sqrt{5}$为边不能组成直角三角形,故本选项不符合题意;
故选B.
点评 本题考查了勾股定理的逆定理,能熟记勾股定理的逆定理的内容是解此题的关键,注意:如果三角形的两边的平方和等于第三边的平方,那么这个三角形是直角三角形.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
11.一组数据4,5,7,7,8,6的中位数和众数分别是( )
| A. | 7,7 | B. | 7,6.5 | C. | 6.5,7 | D. | 5.5,7 |
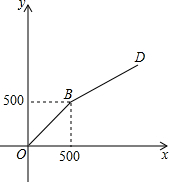 “六一”儿童节期间,甲、乙两家网店以同样价格销售相同的儿童用品,他们的优惠方案分别为:甲店,一次性购物超过100元后的价格部分打七折;乙店,一次性购物超过500元后的价格部分打五折.设商品原价为x元,购物应付金额为y元.
“六一”儿童节期间,甲、乙两家网店以同样价格销售相同的儿童用品,他们的优惠方案分别为:甲店,一次性购物超过100元后的价格部分打七折;乙店,一次性购物超过500元后的价格部分打五折.设商品原价为x元,购物应付金额为y元.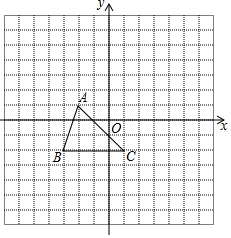 已知:如图,把△A′B′C′向下平移3个单位长度,再向左平移2个单位长度,得到△ABC.
已知:如图,把△A′B′C′向下平移3个单位长度,再向左平移2个单位长度,得到△ABC.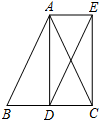 如图,在△ABC中,AB=AC,AD平分∠BAC交BC于点D,分别过点A,D作AE∥BC,DE∥AB,AE与DE相交于点E,连结CE.
如图,在△ABC中,AB=AC,AD平分∠BAC交BC于点D,分别过点A,D作AE∥BC,DE∥AB,AE与DE相交于点E,连结CE.