题目内容
17.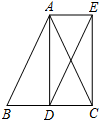 如图,在△ABC中,AB=AC,AD平分∠BAC交BC于点D,分别过点A,D作AE∥BC,DE∥AB,AE与DE相交于点E,连结CE.
如图,在△ABC中,AB=AC,AD平分∠BAC交BC于点D,分别过点A,D作AE∥BC,DE∥AB,AE与DE相交于点E,连结CE.(1)求证:AE=BD;
(2)求证:四边形ADCE是矩形.
分析 (1)先证明四边形ABDE是平行四边形,得出AE=BD即可;
(2)由等腰三角形的性质得出BD=CD,AD⊥BC,得出AE=CD,∠ADC=90°,证出四边形ADCE是平行四边形.即可得出结论.
解答 (1)证明:∵AE∥BC、DE∥AB,
∴四边形ABDE是平行四边形.
∴AE=BD;
(2)证明:由(1)得:AE=BD,
∵AB=AC,AD平分∠BAC,
∴BD=CD,AD⊥BC,
∴AE=CD,∠ADC=90°,
又∵AE∥BC,
∴四边形ADCE是平行四边形.
∴四边形ADCE是矩形.
点评 本题考查了平行四边形的判定与性质、矩形的判定、等腰三角形的性质;熟练掌握平行四边形的判定与性质,由等腰三角形的性质得出BD=CD,AD⊥BC是解决问题的关键.

练习册系列答案
相关题目
5.教育部发布的统计数据显示,近年来越来越多的出国留学人员学成后选择回国发展,留学回国与出国留学人数“逆差”逐渐缩小,2014年各类留学回国人员总数为36.48万人,而2016年各类留学回国人员总数为43.25万人,如果设2014年到2016年各类留学回国人员总数的年平均增长率为x,那么根据题意可列出关于x的方程为( )
| A. | 36.48(1+x)=43.25 | B. | 36.48(1+2x)=43.25 | C. | 36.48(1+x)2=43.25 | D. | 36.48(1-x)2=43.25 |
12.七边形的内角和是( )
| A. | 540° | B. | 720° | C. | 900° | D. | 1080° |
2.下列各组数,可以作为直角三角形的三边长的是( )
| A. | 32,42,52 | B. | $\sqrt{2}$,$\sqrt{2}$,2 | C. | 2,3,4 | D. | $\sqrt{3}$,$\sqrt{4}$,$\sqrt{5}$ |
9.下列调查中,适宜采用全面调查方式的是( )
| A. | 调查乘坐飞机的旅客是否携带了违禁物品 | |
| B. | 调查2017年央视春晚的全国收视率 | |
| C. | 调查某品牌日光灯的使用寿命 | |
| D. | 调查市场上营养快线的质量 |
7.下列图形中不是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
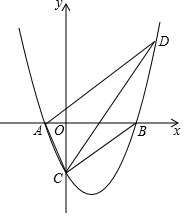 已知抛物线y=ax2+bx-3a与x轴交于A(-1,0),B(x2,0),与y轴负半轴交于点C,OB=OC.
已知抛物线y=ax2+bx-3a与x轴交于A(-1,0),B(x2,0),与y轴负半轴交于点C,OB=OC.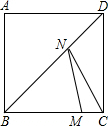 如图,正方形ABCD的边长为8,点M在BC上,且MC=2,N是BD上一动点,则NM+NC的最小值等于10.
如图,正方形ABCD的边长为8,点M在BC上,且MC=2,N是BD上一动点,则NM+NC的最小值等于10.