题目内容
7．在平面直角坐标系中，直线y=4x+2向上平移2个单位长度得到直线m，那么直线m与x轴的交点坐标是（-1，0）．分析 首先求出直线m的解析式为y=4x+2+2，然后再计算出当y=0时，x的值，进而可得直线m与x轴的交点坐标．
解答 解：∵直线y=4x+2向上平移2个单位长度得到直线m，
∴直线m的解析式为y=4x+4，
∵当y=0时，4x+4=0，
解得x=-1，
∴直线m与x轴的交点坐标是（-1，0）．
故答案为：（-1，0）．
点评 此题主要考查了一次函数图象与几何变换，关键是掌握直线y=kx+b向上平移a个单位，则解析式为y=kx+b+a，向下平移a个单位，则解析式为y=kx+b-a．
练习册系列答案
名题训练系列答案
期末集结号系列答案
相关题目
17．已知函数y=（m+1）x+m的函数值y随自变量x的增大而减小，那么m的取值范围是（ ）
| A． | m＞-1 | B． | m＜-1 | C． | m＜1 | D． | m＜0 |
15．在平面直角坐标系中，将点P（3，6）向下平移8个单位后，得到的点位于（ ）
| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
2．下列各组数，可以作为直角三角形的三边长的是（ ）
| A． | 32，42，52 | B． | $\sqrt{2}$，$\sqrt{2}$，2 | C． | 2，3，4 | D． | $\sqrt{3}$，$\sqrt{4}$，$\sqrt{5}$ |
12．
如图，动点P在平面直角坐标系中按图中箭头所示方向运动，第1次从原点运动到点（2，2），第2次接着运动到点（4，0），第3次接着运动到点（6，1），…，按这样的运动规律，经过第72次运动后，动点P的坐标是（ ）
如图，动点P在平面直角坐标系中按图中箭头所示方向运动，第1次从原点运动到点（2，2），第2次接着运动到点（4，0），第3次接着运动到点（6，1），…，按这样的运动规律，经过第72次运动后，动点P的坐标是（ ）| A． | （144，0） | B． | （142，2） | C． | （72，0） | D． | （142，1） |
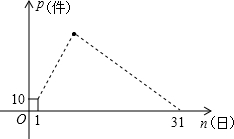3月份，某品牌衬衣正式上市销售，3月1日的销售量为10件，3月2日的销售量为35件，以后每天的销售量比前一天多25件，直到日销售量达到最大后，销售量开始逐日下降，至此，每天的销售量比前一天少15件，直到3月31日销售量为0．设该品牌衬衣的日销量为p（件），销售日期为n（日），p与n之间的关系如图所示．
如图：
17．在平面直角坐标系中，把直线y=x-2向左平移2个单位长度后，其直线解析式为（ ）
| A． | y=x+1 | B． | y=x-1 | C． | y=x | D． | y=x-2 |