题目内容
20．a、b、c是△ABC的三边长，其中a、b满足a2+b2-4a-6b+13=0，则△ABC中最大边c的取值范围是3＜c＜5．．分析 先利用配方法得到（a-2）2+（b-3）2=0，则根据非负数的性质得到a=2，b=3，再根据三角形三边的关系得1＜c＜5，然后根据c为最大边即可得到c的取值范围．
解答 解：a2-4a+4+b2-6b+9=0，
（a-2）2+（b-3）2=0，
a-2=0，b-3=0，
所以a=2，b=3，
所以1＜c＜5，
而c为最大边，
所以3＜c＜5．
故答案为3＜c＜5．
点评 本题考查了因式分解的应用：利用因式分解解决求值问题；利用因式分解解决证明问题；利用因式分解简化计算问题．不要掉了c为最大边的条件．
练习册系列答案
相关题目
11．根据下表回答问题：
（1）272.25的平方根是±16.5
（2）$\sqrt{259.21}$=16.1，$\sqrt{27889}$=167，$\sqrt{2.6244}$=1.62
（3）设$\sqrt{270}$的整数部分为a，求-4a的立方根．
| x | 16 | 16.1 | 16.2 | 16.3 | 16.4 | 16.5 | 16.6 | 16.7 | 16.8 |
| x2 | 256 | 259.21 | 262.44 | 265.69 | 268.96 | 272.25 | 175.56 | 278.89 | 282.24 |
（2）$\sqrt{259.21}$=16.1，$\sqrt{27889}$=167，$\sqrt{2.6244}$=1.62
（3）设$\sqrt{270}$的整数部分为a，求-4a的立方根．
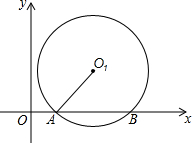如图，⊙O1与x轴交于A（1，0），B（5，0）两点，⊙O1的半径为3．
