题目内容
15.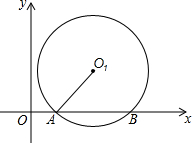 如图,⊙O1与x轴交于A(1,0),B(5,0)两点,⊙O1的半径为3.
如图,⊙O1与x轴交于A(1,0),B(5,0)两点,⊙O1的半径为3.(1)求点O1的坐标;
(2)若将⊙O1上下平移,将⊙O1经过怎样的一次平移后,⊙O1与x轴相切?
分析 (1)作O1D⊥AB于D,交⊙O1于C,根据垂径定理求出AD的长,从而得出OD的长,再由勾股定理求出O1D的长,即可求得点O1的坐标;
(2)根据O1C和O1D的长得出CD的长即可得出结论.
解答 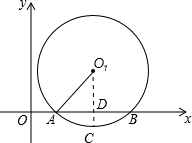 解:(1)作O1D⊥AB于D,交⊙O1于C,
解:(1)作O1D⊥AB于D,交⊙O1于C,
∴AD=BD,
∵A(1,0),B(5,0),
∴AB=4,
∴AD=2,
∴OD=1+2=3,
∵O1A=3,
∴O1D=$\sqrt{{O}_{1}{A}^{2}-{O}_{1}{D}^{2}}$=$\sqrt{5}$,
∴O1(3,$\sqrt{5}$);
(2)∵O1C=3,O1D⊥AB,O1D=$\sqrt{5}$,
∴CD=O1C-O1D=3-$\sqrt{5}$,
∴⊙O1沿OC的方向向上平移3-$\sqrt{5}$个单位时与x轴相切.
点评 本题考查垂径定理、勾股定理、切线的判定、平移的性质,熟知直线与圆相切的条件是解答此题的关键.

练习册系列答案
 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
3.下列计算中,正确的是( )
| A. | $\sqrt{4}=2$ | B. | $\root{3}{9}=3$ | C. | $\root{3}{8}=±2$ | D. | $\sqrt{{{(-3)}^2}}=±3$ |
 如图,已知EF∥CD,∠A=110°,∠EFC=35°,CF为∠ACD的平分线,那么AB与CD平行吗?说明理由.
如图,已知EF∥CD,∠A=110°,∠EFC=35°,CF为∠ACD的平分线,那么AB与CD平行吗?说明理由.