题目内容
4．已知a=2014，b=2015，c=2016，求a2+b2+c2-ab-bc-ac的值．分析 先求出2（a2+b2+c2-ab-bc-ac）的值，再求出a2+b2+c2-ab-bc-ac即可．
解答 解：∵2（a2+b2+c2-ab-bc-ac）
=2a2+2b2+2c2-2ab-2bc-2ac
=（a2-2ab+b2）+（a2-2ac+c2）+（b2-2bc+c2）
=（a-b）2+（a-c）2+（b-c）2
=（2014-2015）2+（2014-2016）2+（2015-2016）2
=1+4+1
=6
∴a2+b2+c2-ab-bc-ac=$\frac{1}{2}$×6=3．
点评 本题主要考查因式分解的应用，能够熟练利用完全平方公式因式分解是解决此题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如图，阴影部分四边形的两个顶点依次在x轴上，其中横坐标分别为1、3、5的顶点A1、A2、A3在一次函数y=2x+5的图象上，横坐标分别为1、3、5的顶点B1、B2、B3在一次函数y=x+3的图象上，记第一个阴影部分四边形面积为S1，第二个阴影部分四边形面积为S2，第三个阴影部分面积为S3，…，则第2015个阴影部分四边形的面积是（ ）
如图，直线DE，FM分别交∠BAC的两边于N，G，P，Q，若∠BNG=115°，∠FPB=65°，DE∥FM吗？如果平行请说明理由．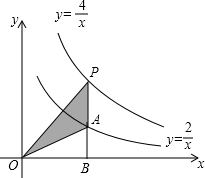
如图，点P是反比例函数y=$\frac{4}{x}$上任意一点，PB⊥x轴交反比例函数y=$\frac{2}{x}$于点A，则△POA的面积为1．
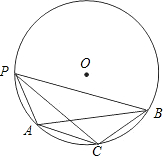如图，点P为⊙O上一点，弦AB=$\sqrt{3}$cm，PC是∠APB的平分线，∠BAC=30°．