题目内容
14. 如图,阴影部分四边形的两个顶点依次在x轴上,其中横坐标分别为1、3、5的顶点A1、A2、A3在一次函数y=2x+5的图象上,横坐标分别为1、3、5的顶点B1、B2、B3在一次函数y=x+3的图象上,记第一个阴影部分四边形面积为S1,第二个阴影部分四边形面积为S2,第三个阴影部分面积为S3,…,则第2015个阴影部分四边形的面积是( )
如图,阴影部分四边形的两个顶点依次在x轴上,其中横坐标分别为1、3、5的顶点A1、A2、A3在一次函数y=2x+5的图象上,横坐标分别为1、3、5的顶点B1、B2、B3在一次函数y=x+3的图象上,记第一个阴影部分四边形面积为S1,第二个阴影部分四边形面积为S2,第三个阴影部分面积为S3,…,则第2015个阴影部分四边形的面积是( )| A. | 2015 | B. | 2017 | C. | 4029 | D. | 4031 |
分析 先分别求出A1、A2、A3,B1、B2、B3的坐标,利用三角形的面积求出S1,S2,S3…,的值,找出规律即可得出结论.
解答 解:∵顶点A1、A2、A3在一次函数y=2x+5的图象上,
∴A1(1,7),A2(3,11),A3(5,15).
∵顶点B1、B2、B3在一次函数y=x+3的图象上,
∴B1(1,4),B2(3,6),A3(5,8),
∴S1=$\frac{1}{2}$×2×(7-4)=3,S2=$\frac{1}{2}$×2×(11-6)=5,S3=$\frac{1}{2}$×2×(15-8)=7…,
∴第2015个阴影部分四边形的面积=2×2015+1=4031.
故选D.
点评 本题考查的是一次函数图象上点的坐标特点,根据题意得出各点坐标,找出三角形面积的规律是解答此题的关键.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
9.函数y=$\frac{x}{x+2}$中自变量x的取值范围是( )
| A. | x≥0 | B. | x<-2 | C. | x>-2 | D. | x≠-2 |
6.单项式$\frac{3x{y}^{2}}{2}$( )
| A. | 它与5πxy2是同类项 | B. | 它的系数为3 | ||
| C. | 它是二次单项式 | D. | 它与-2xy2的和为$\frac{1}{2}$xy2 |
3.下列方程中,属于一元二次方程的是( )
| A. | 10x3=9 | B. | 2(x-1)=3x | C. | x2-1=$\frac{2}{x}$ | D. | (1-x)2=$\frac{1}{2}$ |
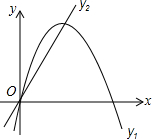 如图,已知抛物线y1=-x2+4x和直线y2=2x.我们约定:当x任取一值时,若y1≠y2,取y1、y2中的较小值记为M;若y1=y2,记M=y1=y2.下列判断:①当x>2时,M=y2;②当x<0时,x值越大,M值越大;③使得M大于4的x值不存在;④若M=2,则x=1.其中正确的说法有②③.(请填写正确说法的番号)
如图,已知抛物线y1=-x2+4x和直线y2=2x.我们约定:当x任取一值时,若y1≠y2,取y1、y2中的较小值记为M;若y1=y2,记M=y1=y2.下列判断:①当x>2时,M=y2;②当x<0时,x值越大,M值越大;③使得M大于4的x值不存在;④若M=2,则x=1.其中正确的说法有②③.(请填写正确说法的番号)
 如图,在△ABC中,AC=BC,分别以点A、C为圆心,大于$\frac{1}{2}$AC的长为半径作弧相交于点M、N,作直线MN,分别交AC、BC于点D、E,连结AE,若△AEB的周长是10,则AB+BC=10.
如图,在△ABC中,AC=BC,分别以点A、C为圆心,大于$\frac{1}{2}$AC的长为半径作弧相交于点M、N,作直线MN,分别交AC、BC于点D、E,连结AE,若△AEB的周长是10,则AB+BC=10.